


Next: Oblique MHD Shocks
Up: Magnetohydrodynamic Fluids
Previous: Parallel MHD Shocks
Perpendicular MHD Shocks
The second special case is the so-called perpendicular MHD shock in which both the
upstream and downstream plasma flows are perpendicular to the magnetic field, as well as the shock
front. In other
words,
Substitution into the general jump conditions (7.250)-(7.255) yields
where
 |
(7.273) |
and  is a real positive root of the quadratic
is a real positive root of the quadratic
![$\displaystyle F(r) = 2\,(2-{\mit\Gamma})\,r^{\,2}+ {\mit\Gamma}\left[2\,(1+\bet...
...ta_1\,M_1^{\,2}\right] r- {\mit\Gamma}\,({\mit\Gamma}+1)\,\beta_1\,M_1^{\,2}=0.$](img2889.png) |
(7.274) |
Here,
 .
.
If 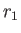 and
and 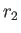 are the two roots of Equation (7.274) then
are the two roots of Equation (7.274) then
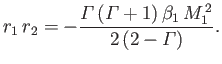 |
(7.275) |
Assuming that
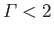 , we conclude that one of the roots is negative,
and, hence, that Equation (7.274) only possesses one physical
solution: that is, there is only one type of MHD shock that is
consistent with Equations (7.269) and (7.270). Now, it is easily
demonstrated that
, we conclude that one of the roots is negative,
and, hence, that Equation (7.274) only possesses one physical
solution: that is, there is only one type of MHD shock that is
consistent with Equations (7.269) and (7.270). Now, it is easily
demonstrated that 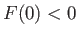 and
and
![$ F[({\mit\Gamma}+1)/({\mit\Gamma}-1)]>0$](img2896.png) . Hence, the
physical root lies between
. Hence, the
physical root lies between  and
and
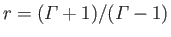 .
.
Using similar analysis to that employed in the previous section, it
can be demonstrated that the second law of thermodynamics requires a
perpendicular shock to be compressive: that is, 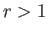 (Boyd and Sanderson 2003). It follows that a physical solution
is only obtained when
(Boyd and Sanderson 2003). It follows that a physical solution
is only obtained when 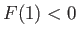 , which reduces to
, which reduces to
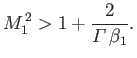 |
(7.276) |
This condition can also be written
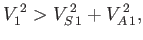 |
(7.277) |
where
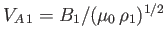 is the upstream
Alfvén velocity. Now,
is the upstream
Alfvén velocity. Now,
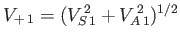 can be recognized as the velocity of a fast wave propagating
perpendicular to the magnetic field. (See Section 7.4.) Thus, the
condition for the existence of a perpendicular shock is that the relative
upstream plasma velocity must be greater than the upstream fast wave velocity. Incidentally, it is easily
demonstrated that if this is the case then the downstream plasma velocity is less than the downstream
fast wave velocity. We can also deduce that, in a stationary plasma, a
perpendicular shock propagates across the magnetic field with
a velocity that exceeds the fast wave velocity.
can be recognized as the velocity of a fast wave propagating
perpendicular to the magnetic field. (See Section 7.4.) Thus, the
condition for the existence of a perpendicular shock is that the relative
upstream plasma velocity must be greater than the upstream fast wave velocity. Incidentally, it is easily
demonstrated that if this is the case then the downstream plasma velocity is less than the downstream
fast wave velocity. We can also deduce that, in a stationary plasma, a
perpendicular shock propagates across the magnetic field with
a velocity that exceeds the fast wave velocity.
In the strong shock limit,  , Equations (7.273) and (7.274) become identical to Equations (7.260) and (7.261).
Hence, a strong perpendicular shock is very similar to a strong hydrodynamic shock (except that the former shock
propagates perpendicular, whereas the latter
shock propagates parallel, to the magnetic field). In particular, just like a hydrodynamic shock, a
perpendicular shock cannot
compress the density by more than a factor
, Equations (7.273) and (7.274) become identical to Equations (7.260) and (7.261).
Hence, a strong perpendicular shock is very similar to a strong hydrodynamic shock (except that the former shock
propagates perpendicular, whereas the latter
shock propagates parallel, to the magnetic field). In particular, just like a hydrodynamic shock, a
perpendicular shock cannot
compress the density by more than a factor
 . However, according to
Equation (7.271), a perpendicular shock compresses the magnetic field by the same
factor that it compresses the plasma density. It follows that there is
also an upper limit to the factor by which a perpendicular shock can compress the magnetic field.
. However, according to
Equation (7.271), a perpendicular shock compresses the magnetic field by the same
factor that it compresses the plasma density. It follows that there is
also an upper limit to the factor by which a perpendicular shock can compress the magnetic field.



Next: Oblique MHD Shocks
Up: Magnetohydrodynamic Fluids
Previous: Parallel MHD Shocks
Richard Fitzpatrick
2016-01-23
![]() and
and ![]() are the two roots of Equation (7.274) then
are the two roots of Equation (7.274) then
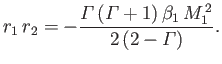
![]() (Boyd and Sanderson 2003). It follows that a physical solution
is only obtained when
(Boyd and Sanderson 2003). It follows that a physical solution
is only obtained when ![]() , which reduces to
, which reduces to
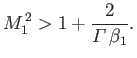
![]() , Equations (7.273) and (7.274) become identical to Equations (7.260) and (7.261).
Hence, a strong perpendicular shock is very similar to a strong hydrodynamic shock (except that the former shock
propagates perpendicular, whereas the latter
shock propagates parallel, to the magnetic field). In particular, just like a hydrodynamic shock, a
perpendicular shock cannot
compress the density by more than a factor
, Equations (7.273) and (7.274) become identical to Equations (7.260) and (7.261).
Hence, a strong perpendicular shock is very similar to a strong hydrodynamic shock (except that the former shock
propagates perpendicular, whereas the latter
shock propagates parallel, to the magnetic field). In particular, just like a hydrodynamic shock, a
perpendicular shock cannot
compress the density by more than a factor
![]() . However, according to
Equation (7.271), a perpendicular shock compresses the magnetic field by the same
factor that it compresses the plasma density. It follows that there is
also an upper limit to the factor by which a perpendicular shock can compress the magnetic field.
. However, according to
Equation (7.271), a perpendicular shock compresses the magnetic field by the same
factor that it compresses the plasma density. It follows that there is
also an upper limit to the factor by which a perpendicular shock can compress the magnetic field.