


Next: Ionospheric Radio Wave Propagation
Up: Wave Propagation in Inhomogeneous
Previous: Total Internal Reflection
Suppose that the region 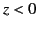 is a vacuum, and the region
is a vacuum, and the region 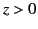 is
occupied by a good conductor of conductivity
is
occupied by a good conductor of conductivity  . Consider a linearly polarized plane wave
normally incident on the interface. Let the wave electric and
magnetic fields in the vacuum region take the form
. Consider a linearly polarized plane wave
normally incident on the interface. Let the wave electric and
magnetic fields in the vacuum region take the form
where
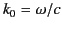 is the vacuum wavenumber. Here,
is the vacuum wavenumber. Here, 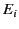 and
and 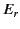 are the amplitudes of the incident and reflected waves,
respectively, whereas
are the amplitudes of the incident and reflected waves,
respectively, whereas
 .
The wave electric and magnetic fields in the conductor are written
.
The wave electric and magnetic fields in the conductor are written
where  is the amplitude of the evanescent wave that penetrates into the
conductor,
is the amplitude of the evanescent wave that penetrates into the
conductor, 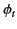 is the phase of this wave with respect to the incident wave,
and
is the phase of this wave with respect to the incident wave,
and
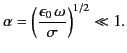 |
(1046) |
The appropriate matching conditions are the continuity of 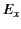 and
and 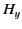 at the vacuum/conductor interface (
at the vacuum/conductor interface (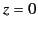 ).
In other words,
).
In other words,
Equations (1049) and (1050), which must be satisfied at all times,
can be solved, in the limit
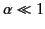 , to give
, to give
Hence, the coefficient of reflection becomes
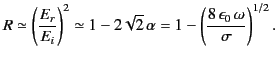 |
(1053) |
According to the previous analysis, a good conductor reflects a normally incident
electromagnetic wave with a phase shift of almost 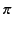 radians (i.e.,
radians (i.e.,
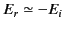 ). The coefficient of reflection is just less than unity, indicating that, while most
of the incident energy is reflected by the conductor, a small fraction of it
is absorbed.
). The coefficient of reflection is just less than unity, indicating that, while most
of the incident energy is reflected by the conductor, a small fraction of it
is absorbed.
High quality metallic mirrors are generally coated in silver, whose conductivity
is
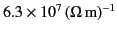 . It follows, from Equation (1055), that at optical
frequencies (
. It follows, from Equation (1055), that at optical
frequencies (
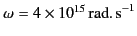 ) the coefficient
of reflection of a silvered mirror is
) the coefficient
of reflection of a silvered mirror is
 percent. This implies that
about
percent. This implies that
about 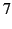 percent of the light incident on the mirror is absorbed, rather than being reflected. This rather severe light loss can be
problematic in instruments, such as astronomical telescopes, that are used to
view faint objects.
percent of the light incident on the mirror is absorbed, rather than being reflected. This rather severe light loss can be
problematic in instruments, such as astronomical telescopes, that are used to
view faint objects.



Next: Ionospheric Radio Wave Propagation
Up: Wave Propagation in Inhomogeneous
Previous: Total Internal Reflection
Richard Fitzpatrick
2014-06-27
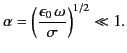
![]() radians (i.e.,
radians (i.e.,
![]() ). The coefficient of reflection is just less than unity, indicating that, while most
of the incident energy is reflected by the conductor, a small fraction of it
is absorbed.
). The coefficient of reflection is just less than unity, indicating that, while most
of the incident energy is reflected by the conductor, a small fraction of it
is absorbed.
![]() . It follows, from Equation (1055), that at optical
frequencies (
. It follows, from Equation (1055), that at optical
frequencies (
![]() ) the coefficient
of reflection of a silvered mirror is
) the coefficient
of reflection of a silvered mirror is
![]() percent. This implies that
about
percent. This implies that
about ![]() percent of the light incident on the mirror is absorbed, rather than being reflected. This rather severe light loss can be
problematic in instruments, such as astronomical telescopes, that are used to
view faint objects.
percent of the light incident on the mirror is absorbed, rather than being reflected. This rather severe light loss can be
problematic in instruments, such as astronomical telescopes, that are used to
view faint objects.