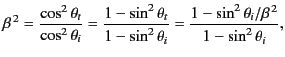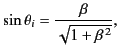Next: Total Internal Reflection
Up: Wave Propagation in Inhomogeneous
Previous: Laws of Geometric Optics
Fresnel Relations
The theory described in the previous section is sufficient to determine the directions of the reflected and refracted waves, when a
light wave is obliquely incident on a plane interface between two dielectric media. However, it cannot determine
the fractions of the incident energy that are reflected and refracted, respectively. In order to calculate the coefficients of reflection and transmission, it is necessary to take into account both the
electric and the magnetic components of the various different waves. It turns out that there are two independent wave polarizations that behave
slightly differently. The first of these is such that the magnetic components of the incident, reflected, and refracted waves are all
parallel to the interface. The second is such that the electric components of these waves are all parallel to the interface.
Consider the first polarization. Let the interface correspond to the plane 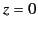 , let the region
, let the region 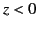 be occupied by material of refractive index
be occupied by material of refractive index 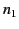 , and let
the region
, and let
the region 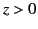 be occupied by material of refractive index
be occupied by material of refractive index  . Suppose that the incident, reflected, and refracted waves are plane waves, of
angular frequency
. Suppose that the incident, reflected, and refracted waves are plane waves, of
angular frequency  , whose wavevectors lie in the
, whose wavevectors lie in the  -
- plane. (See Figure 14.) The equations governing the
propagation of the wave are
plane. (See Figure 14.) The equations governing the
propagation of the wave are
where
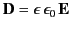 |
(959) |
is the electric displacement, 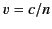 the characteristic wave speed, and
the characteristic wave speed, and
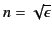 the refractive index. Suppose that, as described in the previous section,
the refractive index. Suppose that, as described in the previous section,
in the region 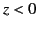 , and
, and
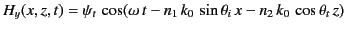 |
(960) |
in the region 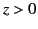 . Here,
. Here,
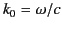 is the vacuum wavenumber,
is the vacuum wavenumber, 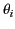 the angle of incidence, and
the angle of incidence, and 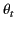 the angle of
refraction. (See Figure 14.) In writing the above expressions, we have made use of the
law of reflection (i.e.,
the angle of
refraction. (See Figure 14.) In writing the above expressions, we have made use of the
law of reflection (i.e.,
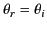 ), as well as the law of refraction (i.e.,
), as well as the law of refraction (i.e.,
 ).
The two terms on the right-hand side of Equation (961) correspond to the incident and reflected waves,
respectively. The term on the right-hand side of Equation (962) corresponds to the refracted wave.
Substitution of Equations (961)-(962) into the governing differential equations, (957)-(959), yields
).
The two terms on the right-hand side of Equation (961) correspond to the incident and reflected waves,
respectively. The term on the right-hand side of Equation (962) corresponds to the refracted wave.
Substitution of Equations (961)-(962) into the governing differential equations, (957)-(959), yields
in the region 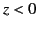 , and
, and
in the region 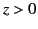 .
.
Now, both the normal and the tangential components of the magnetic
intensity must be continuous at the interface. This implies that
![$\displaystyle [H_y]_{z=0_-}^{z=0_+}=0,$](img2065.png) |
(965) |
which yields
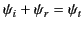 |
(966) |
Furthermore, the normal component of the electric displacement, as well as the tangential
component of the electric field, must be continuous at the interface. In other words,
![$\displaystyle [D_z]_{z=0_-}^{z=0^+} = 0,$](img2067.png) |
(967) |
and
![$\displaystyle [E_x]_{z=0_-}^{z=0_+}=[D_x/(\epsilon\,\epsilon_0)]_{z=0_-}^{z=0_+} = 0.$](img2068.png) |
(968) |
The former of these conditions again gives Equation (968), whereas the latter yields
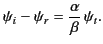 |
(969) |
Here,
It follows that
The electromagnetic energy flux in the  -direction (i.e., normal to the interface) is
-direction (i.e., normal to the interface) is
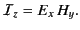 |
(974) |
Thus, the mean energy fluxes associated with the incident, reflected, and refracted
waves are
respectively.
The coefficients of reflection and transmission are defined
respectively.
Hence, it follows that
These expressions are known as Fresnel relations.
Let us now consider the second polarization, in which the electric components of the incident, reflected, and
refracted waves are all parallel to the interface. In this case, the governing equations are
If we make the transformations
 ,
,
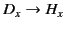 ,
,
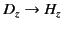 ,
,
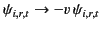 then we can reuse the solutions that we derived for the other polarization.
We find that
then we can reuse the solutions that we derived for the other polarization.
We find that
in the region 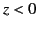 , and
, and
in the region 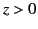 . The first two matching conditions at the interface are that the normal and tangential components of the
magnetic intensity are continuous. In other words,
. The first two matching conditions at the interface are that the normal and tangential components of the
magnetic intensity are continuous. In other words,
The first of these conditions yields
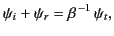 |
(993) |
whereas the second
gives
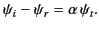 |
(994) |
The final matching condition at the interface is that the tangential component of the electric field is continuous. In other words,
![$\displaystyle [E_y]_{z=0_-}^{z=0_+} = [D_y/(\epsilon\,\epsilon_0)]_{z=0_-}^{z=0_+}=0,$](img2117.png) |
(995) |
which again yields Equation (995).
It follows that
The electromagnetic energy flux in the  -direction is
-direction is
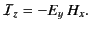 |
(998) |
Thus, the mean energy fluxes associated with the incident, reflected, and refracted
waves are
respectively.
Hence, the coefficients of reflection and transmission are
respectively.
These expressions are the Fresnel relations
for the polarization in which the electric field is parallel to the interface.
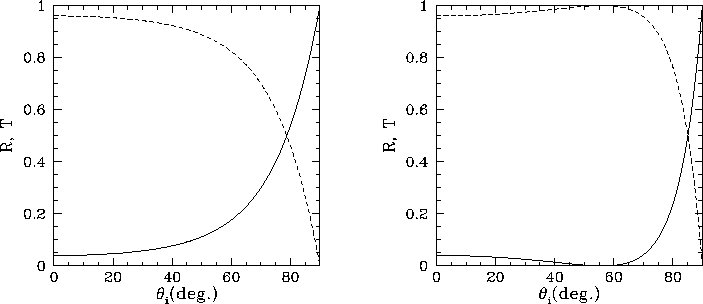
Figure:
Coefficients of reflection (solid curves) and transmission (dashed curves) for oblique incidence from air (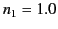 ) to
glass (
) to
glass (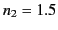 ). The left-hand panel shows the wave polarization
for which the electric field is parallel to the boundary, whereas the
right-hand panel shows the wave polarization for which the
magnetic field is parallel to the boundary. The Brewster angle is
). The left-hand panel shows the wave polarization
for which the electric field is parallel to the boundary, whereas the
right-hand panel shows the wave polarization for which the
magnetic field is parallel to the boundary. The Brewster angle is
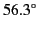 .
.
 |
It can be seen that, at oblique incidence, the Fresnel relations (982) and
(983) for the polarization in which the magnetic
field is parallel to the interface are different to the corresponding relations
(1004) and (1005) for the polarization
in which the electric field is parallel to the interface. This implies that
the coefficients of reflection and transmission for these two polarizations
are, in general, different.
Figure 15 shows the coefficients of reflection and transmission
for oblique incidence from air (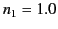 ) to
glass (
) to
glass (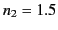 ). Roughly speaking, it can
be seen that the coefficient of reflection rises, and the coefficient of
transmission falls, as the angle of incidence increases. However,
for the polarization in which the magnetic field is parallel to the interface, there is a particular angle of incidence,
know as the Brewster angle, at which the reflected intensity is zero. There is no similar behavior for
the polarization in which the electric field is parallel to the interface.
). Roughly speaking, it can
be seen that the coefficient of reflection rises, and the coefficient of
transmission falls, as the angle of incidence increases. However,
for the polarization in which the magnetic field is parallel to the interface, there is a particular angle of incidence,
know as the Brewster angle, at which the reflected intensity is zero. There is no similar behavior for
the polarization in which the electric field is parallel to the interface.
It follows from Equation (982) that the Brewster angle corresponds
to the condition
 |
(1004) |
or
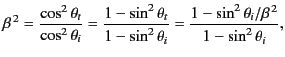 |
(1005) |
where use has been made of Snell's law. The previous expression
reduces to
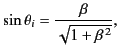 |
(1006) |
or
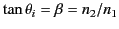 . Hence, the Brewster angle corresponds to
. Hence, the Brewster angle corresponds to
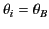 , where
, where
 |
(1007) |
If unpolarized light is incident on an air/glass (say) interface at the Brewster angle
then the reflected light is 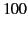 percent linearly polarized. (See Section 7.6.)
percent linearly polarized. (See Section 7.6.)
The fact that the coefficient of reflection for the polarization in which the electric field is parallel to the interface is generally
greater that that for the other polarization (see Figure 15) implies that sunlight reflected from a horizontal water or snow surface is partially linearly polarized, with the horizontal polarization predominating over the vertical one. Such reflected light may be so intense as to cause glare. Polaroid sunglasses help reduce this glare by blocking horizontally polarized light.



Next: Total Internal Reflection
Up: Wave Propagation in Inhomogeneous
Previous: Laws of Geometric Optics
Richard Fitzpatrick
2014-06-27
![]() , let the region
, let the region ![]() be occupied by material of refractive index
be occupied by material of refractive index ![]() , and let
the region
, and let
the region ![]() be occupied by material of refractive index
be occupied by material of refractive index ![]() . Suppose that the incident, reflected, and refracted waves are plane waves, of
angular frequency
. Suppose that the incident, reflected, and refracted waves are plane waves, of
angular frequency ![]() , whose wavevectors lie in the
, whose wavevectors lie in the ![]() -
-![]() plane. (See Figure 14.) The equations governing the
propagation of the wave are
plane. (See Figure 14.) The equations governing the
propagation of the wave are
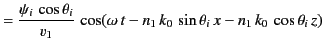
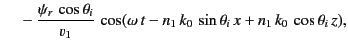
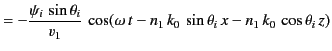
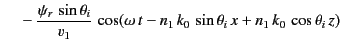
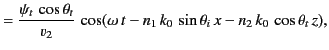

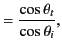
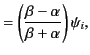
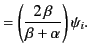
![]() -direction (i.e., normal to the interface) is
-direction (i.e., normal to the interface) is
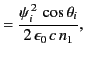
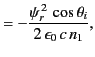
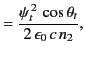
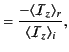
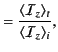
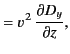
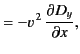
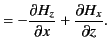
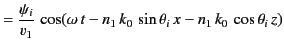

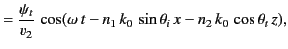
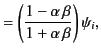
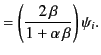
![]() -direction is
-direction is
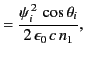
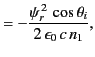
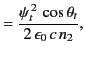

![]() ) to
glass (
) to
glass (![]() ). Roughly speaking, it can
be seen that the coefficient of reflection rises, and the coefficient of
transmission falls, as the angle of incidence increases. However,
for the polarization in which the magnetic field is parallel to the interface, there is a particular angle of incidence,
know as the Brewster angle, at which the reflected intensity is zero. There is no similar behavior for
the polarization in which the electric field is parallel to the interface.
). Roughly speaking, it can
be seen that the coefficient of reflection rises, and the coefficient of
transmission falls, as the angle of incidence increases. However,
for the polarization in which the magnetic field is parallel to the interface, there is a particular angle of incidence,
know as the Brewster angle, at which the reflected intensity is zero. There is no similar behavior for
the polarization in which the electric field is parallel to the interface.