


Next: Exercises
Up: Wave Propagation in Uniform
Previous: Brillouin Precursor
Let us now try to establish at which time, 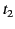 , a signal first arrives
at depth
, a signal first arrives
at depth  inside the dielectric medium whose amplitude is comparable
with that of the wave incident at time
inside the dielectric medium whose amplitude is comparable
with that of the wave incident at time 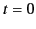 on the surface of the medium
(
on the surface of the medium
(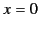 ). Let us term this event the ``arrival'' of the signal.
It is plausible, from the discussion in Section 7.12 regarding the
stationary phase approximation, that signal arrival corresponds to
the situation at which the point of stationary phase in
). Let us term this event the ``arrival'' of the signal.
It is plausible, from the discussion in Section 7.12 regarding the
stationary phase approximation, that signal arrival corresponds to
the situation at which the point of stationary phase in  -space
corresponds to a pole of the function
-space
corresponds to a pole of the function 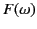 . In other words,
when
. In other words,
when 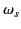 approaches the frequency
approaches the frequency 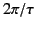 of the incident
signal. It is certainly the case that the stationary phase approximation
yields a particularly large amplitude signal when
of the incident
signal. It is certainly the case that the stationary phase approximation
yields a particularly large amplitude signal when
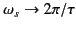 . Unfortunately, as has already been discussed, the method
of stationary phase becomes inaccurate under these circumstances.
However, calculations involving the more robust method of steepest
decent
. Unfortunately, as has already been discussed, the method
of stationary phase becomes inaccurate under these circumstances.
However, calculations involving the more robust method of steepest
decent![[*]](footnote.png) confirm that, in most
cases, the signal amplitude first becomes significant when
confirm that, in most
cases, the signal amplitude first becomes significant when
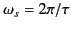 . Thus, the signal arrival time is
. Thus, the signal arrival time is
 |
(944) |
where
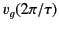 is the group velocity calculated using the
frequency of the incident signal. It is clear from Figure 12 that
is the group velocity calculated using the
frequency of the incident signal. It is clear from Figure 12 that
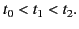 |
(945) |
Thus, the main signal arrives later than the Sommerfeld and Brillouin
precursors.



Next: Exercises
Up: Wave Propagation in Uniform
Previous: Brillouin Precursor
Richard Fitzpatrick
2014-06-27
![[*]](footnote.png) confirm that, in most
cases, the signal amplitude first becomes significant when
confirm that, in most
cases, the signal amplitude first becomes significant when