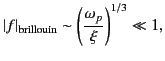Next: Signal Arrival
Up: Wave Propagation in Uniform
Previous: Group Velocity
As time progresses, the horizontal line 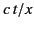 in Figure 12 gradually rises,
and the point of stationary phase moves to ever lower frequencies.
In general, however, the amplitude remains relatively small. Only when
the elapsed time reaches
in Figure 12 gradually rises,
and the point of stationary phase moves to ever lower frequencies.
In general, however, the amplitude remains relatively small. Only when
the elapsed time reaches
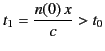 |
(928) |
is there a qualitative change. This time marks the arrival of
a second precursor known as the Brillouin precursor. The reason for
the qualitative change is evident from Figure 12. At 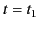 , the lower
region of the
, the lower
region of the 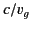 curve is intersected for the first time, and
curve is intersected for the first time, and
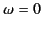 becomes a point of stationary phase. It follows that the
oscillation frequency of the Brillouin precursor is far less than that
of the Sommerfeld precursor. Moreover, it is easily demonstrated that
the second derivative of
becomes a point of stationary phase. It follows that the
oscillation frequency of the Brillouin precursor is far less than that
of the Sommerfeld precursor. Moreover, it is easily demonstrated that
the second derivative of 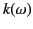 vanishes at
vanishes at 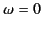 . This means
that
. This means
that
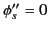 . The stationary phase result (918) gives an
infinite answer in such circumstances. Of course, the amplitude
of the Brillouin precursor is not
infinite, but it is significantly larger than that
of the Sommerfeld precursor.
. The stationary phase result (918) gives an
infinite answer in such circumstances. Of course, the amplitude
of the Brillouin precursor is not
infinite, but it is significantly larger than that
of the Sommerfeld precursor.
In order to generalize the result (918) to deal with a
stationary phase point at 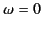 , it is necessary to expand
, it is necessary to expand
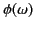 about this point, keeping terms up to
about this point, keeping terms up to
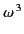 .
Thus,
.
Thus,
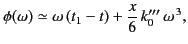 |
(929) |
where
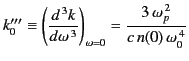 |
(930) |
for the simple dispersion relation (871). The amplitude (910) is
therefore given approximately by
![$\displaystyle f(x,t) \simeq F(0) \int_{\infty}^{-\infty} \exp\left[{\rm i}\,\omega\,(t_1-t) + {\rm i}\,\frac{x}{6} \,k_0'''\, \omega^{\,3}\right]d\omega.$](img1951.png) |
(931) |
This expression reduces to
![$\displaystyle f(x,t) = \frac{\tau}{\sqrt{2}\,\pi^{\,2}}\sqrt{\frac{\vert t-t_1\...
...y \cos\!\left[ \frac{3}{2}\, z\left(\frac{v^{\,3}}{3} \pm v\right) \right]\,dv,$](img1952.png) |
(932) |
where
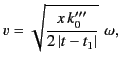 |
(933) |
and
 |
(934) |
The positive (negative) sign in the integrand is taken for 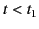 (
(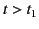 ).
).
The integral in Equation (933) is known as an Airy integral. It can
be expressed in terms of Bessel functions of order 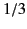 , as follows:
, as follows:
![$\displaystyle \int_0^\infty \cos\!\left[ \frac{3}{2} \,z\left(\frac{v^{\,3}}{3} + v\right) \right]\,dv= \frac{1}{\sqrt{3}} \,K_{1/3}(z),$](img1958.png) |
(935) |
and
![$\displaystyle \int_0^\infty \cos\!\left[ \frac{3}{2}\, z\left(\frac{v^{\,3}}{3} - v\right) \right]\,dv= \frac{\pi}{3} \left[ J_{1/3}(z) + J_{-1/3}(z)\right].$](img1959.png) |
(936) |
From the well-known properties of Bessel functions, the precursor
can be seen to have a growing exponential character for
times earlier than 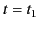 , and an oscillating character for
, and an oscillating character for
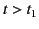 . The amplitude in the neighborhood of
. The amplitude in the neighborhood of 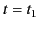 is plotted
in Figure 13.
is plotted
in Figure 13.
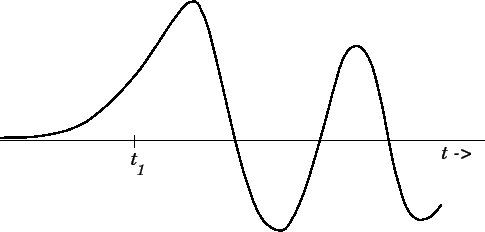
Figure 13:
A sketch of the behavior of the Brillouin precursor as a function
of time.
 |
The initial oscillation period of the Brillouin precursor is
crudely estimated (by setting 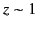 ) as
) as
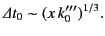 |
(937) |
The amplitude of the Brillouin precursor is approximately
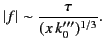 |
(938) |
Let us adopt the ordering
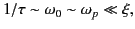 |
(939) |
which corresponds to the majority of physical situations involving the propagation
of electromagnetic radiation through dielectric media. It follows, from the
previous results, plus the results of Section 7.11, that
 |
(940) |
and
 |
(941) |
Furthermore,
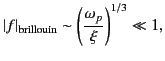 |
(942) |
and
 |
(943) |
Thus, it is clear that the Sommerfeld precursor is essentially a low amplitude, high
frequency signal, whereas the Brillouin precursor is a high amplitude,
low frequency signal. Note that the amplitude of the Brillouin precursor,
despite being significantly higher than that of the Sommerfeld
precursor, is still much less than that of the incident wave.



Next: Signal Arrival
Up: Wave Propagation in Uniform
Previous: Group Velocity
Richard Fitzpatrick
2014-06-27
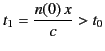
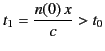
![]() , it is necessary to expand
, it is necessary to expand
![]() about this point, keeping terms up to
about this point, keeping terms up to
![]() .
Thus,
.
Thus,
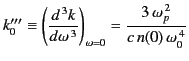
![$\displaystyle f(x,t) \simeq F(0) \int_{\infty}^{-\infty} \exp\left[{\rm i}\,\omega\,(t_1-t) + {\rm i}\,\frac{x}{6} \,k_0'''\, \omega^{\,3}\right]d\omega.$](img1951.png)
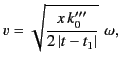

![]() , as follows:
, as follows:
![$\displaystyle \int_0^\infty \cos\!\left[ \frac{3}{2} \,z\left(\frac{v^{\,3}}{3} + v\right) \right]\,dv= \frac{1}{\sqrt{3}} \,K_{1/3}(z),$](img1958.png)
![$\displaystyle \int_0^\infty \cos\!\left[ \frac{3}{2}\, z\left(\frac{v^{\,3}}{3} - v\right) \right]\,dv= \frac{\pi}{3} \left[ J_{1/3}(z) + J_{-1/3}(z)\right].$](img1959.png)
![]() ) as
) as