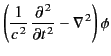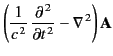Next: Retarded Fields
Up: Maxwell's Equations
Previous: Solution of Inhomogeneous Wave
We are now in a position to solve Maxwell's equations. Recall, from Section 1.3, that Maxwell equations reduce to
We can solve these inhomogeneous three-dimensional waves equations using the appropriate Green's function, (49).
In fact, making use of Equation (46),
we find that
Alternatively, we can write
The above potentials are termed retarded potentials (because the
integrands are evaluated at the retarded time). Finally, according to the discussion in the previous section, we can be sure that Equations (75)
and (76) are the unique solutions to Equations (71) and (72), respectively, subject to sensible boundary conditions
at infinity.



Next: Retarded Fields
Up: Maxwell's Equations
Previous: Solution of Inhomogeneous Wave
Richard Fitzpatrick
2014-06-27