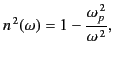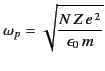Next: Polarization of Electromagnetic Waves
Up: Wave Propagation in Uniform
Previous: Wave Propagation in Conducting
Consider the behavior of the dispersion relation (786) in the
high frequency limit
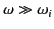 (for all
(for all 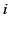 ). In this
case, the relation simplifies considerably to give
). In this
case, the relation simplifies considerably to give
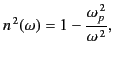 |
(810) |
where the quantity
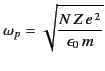 |
(811) |
is called the plasma frequency. The wavenumber in the high frequency
limit is given by
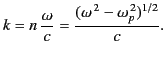 |
(812) |
This expression is only valid in dielectrics when
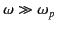 .
Thus, the refractive index is real, and slightly less than unity, giving
waves that propagate without attenuation at a phase velocity slightly
larger than the velocity of light in vacuum. However, in certain ionized
media
(in particular, in tenuous plasmas, such as occur in the ionosphere) the
electrons are free, and the damping is negligible. In this case,
Equations (811) and (813) are valid even when
.
Thus, the refractive index is real, and slightly less than unity, giving
waves that propagate without attenuation at a phase velocity slightly
larger than the velocity of light in vacuum. However, in certain ionized
media
(in particular, in tenuous plasmas, such as occur in the ionosphere) the
electrons are free, and the damping is negligible. In this case,
Equations (811) and (813) are valid even when
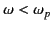 . It follows that a wave can only propagate through a tenuous plasma when its
frequency exceeds the plasma frequency (in which case, it has a real
wavenumber). If wave frequency is less than the plasma frequency then, according to Equation (813), the
wavenumber is purely imaginary,
and the wave is unable to propagate. This phenomenon accounts for the fact that
long-wave and medium-wave (terrestrial) radio signals can be received even when the transmitter lies over the horizon. The frequency of these waves is less than the
plasma frequency of the ionosphere, which reflects them (see Chapter 8),
so they become trapped between the
ionosphere and the surface of the Earth (which is also a good reflector of
radio waves), and can, in certain cases, travel many times around the Earth
before being attenuated. Unfortunately, this scheme does not work
very well for medium-wave signals at night. The problem is that the
plasma frequency of the ionosphere is proportional to the square root of the
number density of free ionospheric electrons. These free electrons are
generated through the ionization of neutral molecules by ultraviolet radiation
from the Sun. Of course, there is no radiation from the Sun at night, so
the density of free electrons starts to drop as the electrons gradually
recombine with ions in the ionosphere. Eventually, the plasma frequency of
the ionosphere falls below the frequency of medium-wave radio signals,
causing them to be transmitted through the ionosphere into outer space.
The ionosphere appears almost completely
transparent to high frequency signals such as
TV and FM radio signals. Thus, this type of signal is not reflected by
the ionosphere. Consequently, to receive such signals it is necessary to
be in the line of sight of the relevant transmitter.
. It follows that a wave can only propagate through a tenuous plasma when its
frequency exceeds the plasma frequency (in which case, it has a real
wavenumber). If wave frequency is less than the plasma frequency then, according to Equation (813), the
wavenumber is purely imaginary,
and the wave is unable to propagate. This phenomenon accounts for the fact that
long-wave and medium-wave (terrestrial) radio signals can be received even when the transmitter lies over the horizon. The frequency of these waves is less than the
plasma frequency of the ionosphere, which reflects them (see Chapter 8),
so they become trapped between the
ionosphere and the surface of the Earth (which is also a good reflector of
radio waves), and can, in certain cases, travel many times around the Earth
before being attenuated. Unfortunately, this scheme does not work
very well for medium-wave signals at night. The problem is that the
plasma frequency of the ionosphere is proportional to the square root of the
number density of free ionospheric electrons. These free electrons are
generated through the ionization of neutral molecules by ultraviolet radiation
from the Sun. Of course, there is no radiation from the Sun at night, so
the density of free electrons starts to drop as the electrons gradually
recombine with ions in the ionosphere. Eventually, the plasma frequency of
the ionosphere falls below the frequency of medium-wave radio signals,
causing them to be transmitted through the ionosphere into outer space.
The ionosphere appears almost completely
transparent to high frequency signals such as
TV and FM radio signals. Thus, this type of signal is not reflected by
the ionosphere. Consequently, to receive such signals it is necessary to
be in the line of sight of the relevant transmitter.



Next: Polarization of Electromagnetic Waves
Up: Wave Propagation in Uniform
Previous: Wave Propagation in Conducting
Richard Fitzpatrick
2014-06-27