


Next: Wave Propagation in Conducting
Up: Wave Propagation in Uniform
Previous: Form of Dielectric Constant
Anomalous Dispersion and Resonant Absorption
When 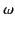 is approximately equal to
is approximately equal to 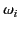 , the
dispersion relation (786) reduces to
, the
dispersion relation (786) reduces to
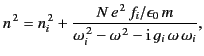 |
(787) |
where 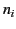 is the average contribution in the vicinity of
is the average contribution in the vicinity of
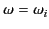 of all the other resonances (also included in
of all the other resonances (also included in 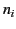 is the contribution 1
of the vacuum displacement current, which was previously written separately). The refractive index is clearly complex.
For a wave propagating in the
is the contribution 1
of the vacuum displacement current, which was previously written separately). The refractive index is clearly complex.
For a wave propagating in the 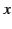 -direction,
-direction,
![$\displaystyle {\bf E} = {\bf E}_0 \,\exp[\,{\rm i}\,(\omega/c)\,({\rm Re}(n)\,x-c \,t)] \exp[-(\omega/c)\,{\rm Im}(n)\,x].$](img1643.png) |
(788) |
Thus, the phase velocity of the wave is determined by the real part of
the refractive index via
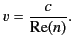 |
(789) |
Furthermore, a positive imaginary component of the refractive index leads to the
attenuation of the wave as it propagates.
Let
where 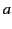 ,
, 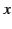 ,
, 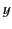 ,
, 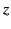 are all dimensionless quantities. It follows from Equation (788)
that
are all dimensionless quantities. It follows from Equation (788)
that
Let us adopt the physical ordering 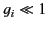 . In this case, the extrema of the
function
. In this case, the extrema of the
function 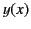 occur at
occur at
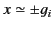 . In fact, it is easily demonstrated that
. In fact, it is easily demonstrated that
The maximum value of the function 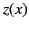 occurs at
occurs at 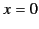 . In fact,
. In fact,
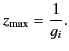 |
(798) |
Note also that
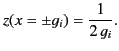 |
(799) |
Figure:
Sketch of the variation of the functions 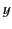 and
and 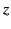 with
with 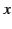 . The solid and dashed curves shows
. The solid and dashed curves shows 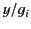 and
and 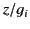 ,
respectively.
,
respectively.
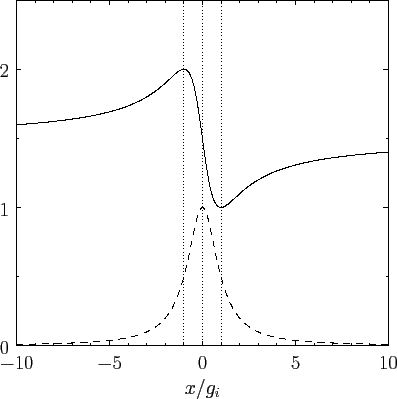 |
Figure 5 shows a sketch of the functions 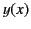 and
and 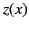 . These curves are also indicative of the variation of
. These curves are also indicative of the variation of
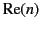 and
and
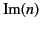 , respectively, with frequency,
, respectively, with frequency,
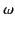 , in the vicinity
of the resonant frequency,
, in the vicinity
of the resonant frequency, 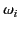 . Recall that normal dispersion
is associated with an increase in
. Recall that normal dispersion
is associated with an increase in
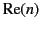 with increasing
with increasing 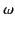 .
The reverse situation is termed anomalous dispersion. It is
clear, from the figure, that normal dispersion occurs everywhere, except at wave frequencies in the
immediate neighborhood of the resonant frequency,
.
The reverse situation is termed anomalous dispersion. It is
clear, from the figure, that normal dispersion occurs everywhere, except at wave frequencies in the
immediate neighborhood of the resonant frequency, 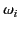 . It is
also clear
that the imaginary part of the refractive index is only appreciable
in those regions of the electromagnetic spectrum where anomalous dispersion
takes place.
A positive imaginary component of the refractive index implies
that the wave is absorbed as it propagates through the medium.
Consequently, the regions
of the spectrum in which
. It is
also clear
that the imaginary part of the refractive index is only appreciable
in those regions of the electromagnetic spectrum where anomalous dispersion
takes place.
A positive imaginary component of the refractive index implies
that the wave is absorbed as it propagates through the medium.
Consequently, the regions
of the spectrum in which
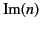 is appreciable are called regions
of resonant absorption. Anomalous dispersion and resonant
absorption take place in the vicinity of the
is appreciable are called regions
of resonant absorption. Anomalous dispersion and resonant
absorption take place in the vicinity of the 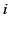 th resonance when
th resonance when
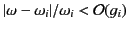 . Because the damping constants,
. Because the damping constants, 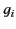 , are,
in practice, very small compared to unity, the regions of the spectrum
in which resonant absorption takes place are strongly
localized in the vicinity
of the various resonant frequencies.
, are,
in practice, very small compared to unity, the regions of the spectrum
in which resonant absorption takes place are strongly
localized in the vicinity
of the various resonant frequencies.
The dispersion relation (786) only takes electron resonances into
account. Of course, there are also resonances associated with displacements
of the ions (or atomic nuclei). The off-resonance contributions to
the right-hand side of Equation (786) from the ions are typically smaller than those
from the electrons by a factor of order 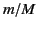 (where
(where 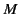 is a typical
ion mass). Nevertheless, the ion contributions are important,
because they give rise to anomalous dispersion and
resonant absorption close to the ion
resonant frequencies. The ion resonances associated with the stretching and
bending of molecular bonds usually lie in the infrared region of
the electromagnetic spectrum. Those resonances associated with molecular rotation (which
only affect the dispersion relation if the molecule is polar) occur in the
microwave region of the spectrum. Both air and water exhibit
strong resonant absorption of electromagnetic waves in both the
ultraviolet and infrared regions of the spectrum. In the former case, this
is due to electron resonances, and in the latter to ion resonances.
The visible region of the spectrum exists as a narrow window,
lying between these two regions, in which there is comparatively little attenuation
of electromagnetic waves.
is a typical
ion mass). Nevertheless, the ion contributions are important,
because they give rise to anomalous dispersion and
resonant absorption close to the ion
resonant frequencies. The ion resonances associated with the stretching and
bending of molecular bonds usually lie in the infrared region of
the electromagnetic spectrum. Those resonances associated with molecular rotation (which
only affect the dispersion relation if the molecule is polar) occur in the
microwave region of the spectrum. Both air and water exhibit
strong resonant absorption of electromagnetic waves in both the
ultraviolet and infrared regions of the spectrum. In the former case, this
is due to electron resonances, and in the latter to ion resonances.
The visible region of the spectrum exists as a narrow window,
lying between these two regions, in which there is comparatively little attenuation
of electromagnetic waves.



Next: Wave Propagation in Conducting
Up: Wave Propagation in Uniform
Previous: Form of Dielectric Constant
Richard Fitzpatrick
2014-06-27
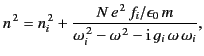
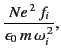
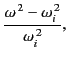
![$\displaystyle \frac{[{\rm Re}(n)]^{\,2} - [{\rm Im}(n)]^{\,2}}{a^{\,2}},$](img1650.png)
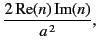
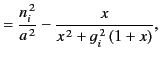
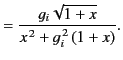
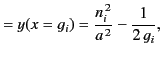
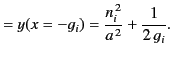
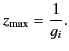
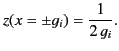

![]() and
and ![]() . These curves are also indicative of the variation of
. These curves are also indicative of the variation of
![]() and
and
![]() , respectively, with frequency,
, respectively, with frequency,
![]() , in the vicinity
of the resonant frequency,
, in the vicinity
of the resonant frequency, ![]() . Recall that normal dispersion
is associated with an increase in
. Recall that normal dispersion
is associated with an increase in
![]() with increasing
with increasing ![]() .
The reverse situation is termed anomalous dispersion. It is
clear, from the figure, that normal dispersion occurs everywhere, except at wave frequencies in the
immediate neighborhood of the resonant frequency,
.
The reverse situation is termed anomalous dispersion. It is
clear, from the figure, that normal dispersion occurs everywhere, except at wave frequencies in the
immediate neighborhood of the resonant frequency, ![]() . It is
also clear
that the imaginary part of the refractive index is only appreciable
in those regions of the electromagnetic spectrum where anomalous dispersion
takes place.
A positive imaginary component of the refractive index implies
that the wave is absorbed as it propagates through the medium.
Consequently, the regions
of the spectrum in which
. It is
also clear
that the imaginary part of the refractive index is only appreciable
in those regions of the electromagnetic spectrum where anomalous dispersion
takes place.
A positive imaginary component of the refractive index implies
that the wave is absorbed as it propagates through the medium.
Consequently, the regions
of the spectrum in which
![]() is appreciable are called regions
of resonant absorption. Anomalous dispersion and resonant
absorption take place in the vicinity of the
is appreciable are called regions
of resonant absorption. Anomalous dispersion and resonant
absorption take place in the vicinity of the ![]() th resonance when
th resonance when
![]() . Because the damping constants,
. Because the damping constants, ![]() , are,
in practice, very small compared to unity, the regions of the spectrum
in which resonant absorption takes place are strongly
localized in the vicinity
of the various resonant frequencies.
, are,
in practice, very small compared to unity, the regions of the spectrum
in which resonant absorption takes place are strongly
localized in the vicinity
of the various resonant frequencies.
![]() (where
(where ![]() is a typical
ion mass). Nevertheless, the ion contributions are important,
because they give rise to anomalous dispersion and
resonant absorption close to the ion
resonant frequencies. The ion resonances associated with the stretching and
bending of molecular bonds usually lie in the infrared region of
the electromagnetic spectrum. Those resonances associated with molecular rotation (which
only affect the dispersion relation if the molecule is polar) occur in the
microwave region of the spectrum. Both air and water exhibit
strong resonant absorption of electromagnetic waves in both the
ultraviolet and infrared regions of the spectrum. In the former case, this
is due to electron resonances, and in the latter to ion resonances.
The visible region of the spectrum exists as a narrow window,
lying between these two regions, in which there is comparatively little attenuation
of electromagnetic waves.
is a typical
ion mass). Nevertheless, the ion contributions are important,
because they give rise to anomalous dispersion and
resonant absorption close to the ion
resonant frequencies. The ion resonances associated with the stretching and
bending of molecular bonds usually lie in the infrared region of
the electromagnetic spectrum. Those resonances associated with molecular rotation (which
only affect the dispersion relation if the molecule is polar) occur in the
microwave region of the spectrum. Both air and water exhibit
strong resonant absorption of electromagnetic waves in both the
ultraviolet and infrared regions of the spectrum. In the former case, this
is due to electron resonances, and in the latter to ion resonances.
The visible region of the spectrum exists as a narrow window,
lying between these two regions, in which there is comparatively little attenuation
of electromagnetic waves.