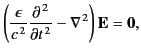 |
(767) |
In some dielectric media, the dielectric constant, ![]() , is complex. According to Equation (772), this leads
to a complex wavevector,
, is complex. According to Equation (772), this leads
to a complex wavevector, ![]() (assuming that the angular frequency is real). Thus, for a wave propagating in the
(assuming that the angular frequency is real). Thus, for a wave propagating in the ![]() -direction, we obtain
-direction, we obtain
Up to now, we have tacitly assumed that ![]() is the same for waves of
all frequencies. In practice,
is the same for waves of
all frequencies. In practice, ![]() varies (in some cases, strongly)
with the wave frequency. Consequently, waves of different frequencies
propagate through a dielectric medium at different phase velocities, leading to the dispersion of wave pulses.
Moreover, there may exist frequency
bands in which
the waves are attenuated (i.e., absorbed). All of this makes the problem of determining
the behavior of a wave pulse as it propagates through a dielectric
medium a
far from straightforward task. Of course, the solution to this problem
for a wave pulse traveling through a vacuum is fairly trivial: that is,
the pulse propagates at the velocity
varies (in some cases, strongly)
with the wave frequency. Consequently, waves of different frequencies
propagate through a dielectric medium at different phase velocities, leading to the dispersion of wave pulses.
Moreover, there may exist frequency
bands in which
the waves are attenuated (i.e., absorbed). All of this makes the problem of determining
the behavior of a wave pulse as it propagates through a dielectric
medium a
far from straightforward task. Of course, the solution to this problem
for a wave pulse traveling through a vacuum is fairly trivial: that is,
the pulse propagates at the velocity ![]() without changing shape. What is the equivalent result for
the case of a dielectric medium? This is a significant question, because
most of our information regarding the universe is obtained from
the study of electromagnetic waves emitted by distant objects.
All of these waves have to propagate through dispersive media (e.g.,
the interstellar medium, the ionosphere, the atmosphere) before reaching
us. It is, therefore, vitally important that we understand which aspects
of these wave signals
are predominantly determined by the wave sources, and which
are strongly modified by the dispersive media through which the signals have
propagated in order to reach us.
without changing shape. What is the equivalent result for
the case of a dielectric medium? This is a significant question, because
most of our information regarding the universe is obtained from
the study of electromagnetic waves emitted by distant objects.
All of these waves have to propagate through dispersive media (e.g.,
the interstellar medium, the ionosphere, the atmosphere) before reaching
us. It is, therefore, vitally important that we understand which aspects
of these wave signals
are predominantly determined by the wave sources, and which
are strongly modified by the dispersive media through which the signals have
propagated in order to reach us.