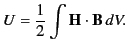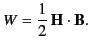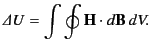Next: Exercises
Up: Magnetostatics in Magnetic Media
Previous: Magnetic Shielding
Consider an electrical conductor. Suppose that a battery with an
electromotive field 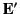 is feeding energy into this conductor.
The energy is either dissipated as heat, or is used to generate a
magnetic field. Ohm's law inside the conductor gives
is feeding energy into this conductor.
The energy is either dissipated as heat, or is used to generate a
magnetic field. Ohm's law inside the conductor gives
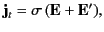 |
(757) |
where 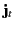 is the true current density,
is the true current density, 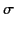 is the
conductivity, and
is the
conductivity, and 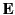 is the inductive electric field. Taking
the scalar product with
is the inductive electric field. Taking
the scalar product with 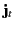 , we obtain
, we obtain
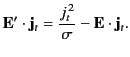 |
(758) |
The left-hand side of this equation represents the rate at which the
battery does work on the conductor. The first term on the right-hand
side is the rate of Joule heating inside the conductor. We tentatively
identify the remaining term with the rate at which energy is fed into
the magnetic field. If all fields are quasi-stationary
(i.e., slowly varying) then the displacement current can be neglected,
and Equation (688) reduces to
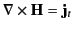 . Substituting this expression into Equation (759)
and integrating over all space, we get
. Substituting this expression into Equation (759)
and integrating over all space, we get
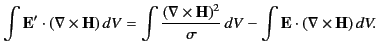 |
(759) |
The last term can be integrated by parts using the identity
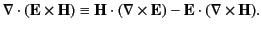 |
(760) |
Making use of the divergence theorem, as well as Equation (3), we get
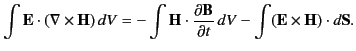 |
(761) |
Because
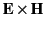 falls off at least as fast as
falls off at least as fast as 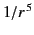 in
electrostatic and quasi-stationary magnetic fields (
in
electrostatic and quasi-stationary magnetic fields (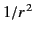 comes from electric
monopole fields, and
comes from electric
monopole fields, and 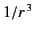 from magnetic dipole fields), the surface
integral in the previous expression can be neglected. Of course, this is
not the case for radiation fields, for which
from magnetic dipole fields), the surface
integral in the previous expression can be neglected. Of course, this is
not the case for radiation fields, for which 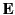 and
and  fall off like
fall off like 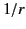 . (See Section 1.8.) Thus, the constraint of ``quasi-stationarity'' effectively
means that the fields vary sufficiently slowly that any radiation fields
can be neglected.
. (See Section 1.8.) Thus, the constraint of ``quasi-stationarity'' effectively
means that the fields vary sufficiently slowly that any radiation fields
can be neglected.
The total power expended by the battery can now be written
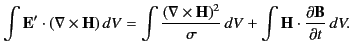 |
(762) |
The first term on the right-hand side has already been identified as the
energy
loss rate due to Joule heating. The last term is obviously the
rate at which energy is fed into the magnetic field. The variation
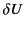 in the magnetic field energy can therefore be written
in the magnetic field energy can therefore be written
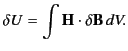 |
(763) |
In order to make Equation (764) integrable, we must assume a functional
relationship between  and
and 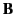 . For a medium that
magnetizes linearly, the integration can be carried out, in much the
same manner as Equation (567), to give
. For a medium that
magnetizes linearly, the integration can be carried out, in much the
same manner as Equation (567), to give
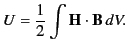 |
(764) |
Thus, the magnetostatic energy density inside a linear magnetic
material is given by
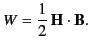 |
(765) |
Unfortunately, most interesting magnetic materials, such as ferromagnets,
exhibit a nonlinear relationship between  and
and 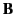 .
For such materials, Equation (764) can only be integrated between
definite states, and the result, in general, depends on the past
history of the sample. For ferromagnets, the integral of Equation (764) has
a finite, non-zero value when
.
For such materials, Equation (764) can only be integrated between
definite states, and the result, in general, depends on the past
history of the sample. For ferromagnets, the integral of Equation (764) has
a finite, non-zero value when 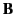 is integrated around a
complete magnetization cycle. This cyclic energy loss
is given by
is integrated around a
complete magnetization cycle. This cyclic energy loss
is given by
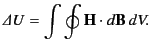 |
(766) |
In other words, the energy expended per unit volume when a magnetic
material is carried through a magnetization cycle is equal to the area of
its hysteresis loop as plotted in a graph of 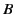 against
against 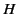 . Thus,
it is particularly important to ensure that the magnetic used to form
transformer cores possess hysteresis loops with comparatively small
areas, otherwise the transformers are likely to be extremely inefficient.
. Thus,
it is particularly important to ensure that the magnetic used to form
transformer cores possess hysteresis loops with comparatively small
areas, otherwise the transformers are likely to be extremely inefficient.



Next: Exercises
Up: Magnetostatics in Magnetic Media
Previous: Magnetic Shielding
Richard Fitzpatrick
2014-06-27
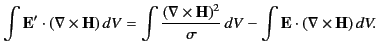
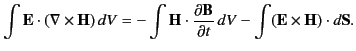
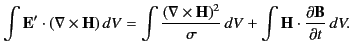
![]() and
and ![]() . For a medium that
magnetizes linearly, the integration can be carried out, in much the
same manner as Equation (567), to give
. For a medium that
magnetizes linearly, the integration can be carried out, in much the
same manner as Equation (567), to give