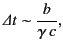Next: Relativistic Particle Dynamics
Up: Relativity and Electromagnetism
Previous: Potential Due to a
Field Due to a Moving Charge
Although the fields generated by a uniformly moving charge can be calculated
from the expressions (1822) and (1823) for the potentials, it is simpler to
calculate them from first principles.
Let a charge 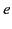 , whose position vector at time
, whose position vector at time 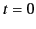 is
is 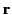 , move with
uniform velocity
, move with
uniform velocity 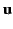 in a frame
in a frame 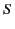 whose
whose 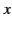 -axis has been chosen
in the direction of
-axis has been chosen
in the direction of 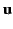 . We require to find the field strengths
. We require to find the field strengths
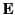 and
and 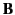 at the event
at the event
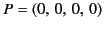 . Let
. Let 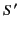 be that frame
in standard configuration with
be that frame
in standard configuration with 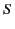 in which the charge is permanently at
rest. In
in which the charge is permanently at
rest. In 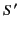 , the field is given by
, the field is given by
This field must now be transformed into the frame 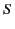 . The direct method,
using Equations (1809)-(1812), is somewhat simpler here, but we shall use a somewhat
indirect method because of its intrinsic interest.
. The direct method,
using Equations (1809)-(1812), is somewhat simpler here, but we shall use a somewhat
indirect method because of its intrinsic interest.
In order to express Equations (1825) and (1826) in tensor form, we need the electromagnetic
field tensor
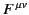 on the left-hand side, and the position 4-vector
on the left-hand side, and the position 4-vector
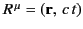 and the scalar
and the scalar
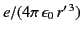 on the right-hand side. (We regard
on the right-hand side. (We regard 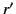 as an invariant for all observers.)
To get a vanishing magnetic field in
as an invariant for all observers.)
To get a vanishing magnetic field in  , we multiply on the right
by the 4-velocity
, we multiply on the right
by the 4-velocity
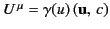 , thus tentatively
arriving at the equation
, thus tentatively
arriving at the equation
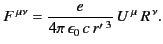 |
(1825) |
Recall that
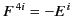 and
and
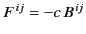 . However, this equation
cannot be correct, because the antisymmetric tensor
. However, this equation
cannot be correct, because the antisymmetric tensor
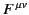 can only be equated to another antisymmetric tensor. Consequently,
let us try
can only be equated to another antisymmetric tensor. Consequently,
let us try
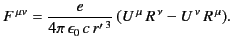 |
(1826) |
This is found to give the correct field at 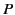 in
in 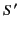 , as long as
, as long as
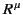 refers to any event whatsoever at the charge.
It only remains to interpret Equation (1828) in
refers to any event whatsoever at the charge.
It only remains to interpret Equation (1828) in 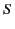 . It is convenient to choose for
. It is convenient to choose for
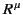 that event at the charge at which
that event at the charge at which 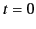 (not the
retarded event). Thus,
(not the
retarded event). Thus,
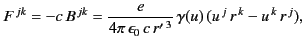 |
(1827) |
giving
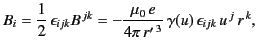 |
(1828) |
or
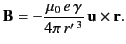 |
(1829) |
Likewise,
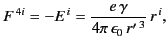 |
(1830) |
or
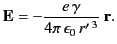 |
(1831) |
Lastly, we must find an expression for
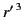 in terms of quantities
measured in
in terms of quantities
measured in 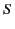 at time
at time 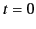 . If
. If 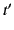 is the corresponding time in
is the corresponding time in 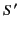 at the charge then we have
at the charge then we have
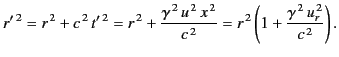 |
(1832) |
Thus,
Note that 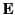 acts in line with the point which the charge
occupies at the instant of measurement, despite the fact that,
owing to the finite speed of propagation of all physical effects,
the behavior of the charge during a finite period before that instant
can no longer affect the measurement. Note also that, unlike
Equations (1822) and (1823), the previous expressions for the fields are not valid for
an arbitrarily moving charge, nor can they be made valid by merely using
retarded values. For whereas acceleration does not affect the potentials,
it does affect the fields, which involve the derivatives of the potential.
acts in line with the point which the charge
occupies at the instant of measurement, despite the fact that,
owing to the finite speed of propagation of all physical effects,
the behavior of the charge during a finite period before that instant
can no longer affect the measurement. Note also that, unlike
Equations (1822) and (1823), the previous expressions for the fields are not valid for
an arbitrarily moving charge, nor can they be made valid by merely using
retarded values. For whereas acceleration does not affect the potentials,
it does affect the fields, which involve the derivatives of the potential.
For low velocities,
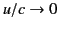 , Equations (1835) and (1836) reduce to the
well-known Coulomb and Biot-Savart fields. However, at high
velocities,
, Equations (1835) and (1836) reduce to the
well-known Coulomb and Biot-Savart fields. However, at high
velocities,
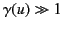 , the fields exhibit some interesting behavior.
The peak electric field, which occurs at the point of closest approach
of the charge to the observation point, becomes equal to
, the fields exhibit some interesting behavior.
The peak electric field, which occurs at the point of closest approach
of the charge to the observation point, becomes equal to 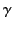 times
its non-relativistic value. However, the duration of appreciable
field strength at the point
times
its non-relativistic value. However, the duration of appreciable
field strength at the point 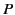 is decreased. A measure of the time
interval over which the field is appreciable is
is decreased. A measure of the time
interval over which the field is appreciable is
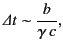 |
(1835) |
where 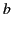 is the distance of closest approach (assuming
is the distance of closest approach (assuming
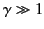 ). As
). As 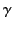 increases, the
peak field increases in proportion, but its duration goes in the
inverse proportion. The time integral of the field
is independent of
increases, the
peak field increases in proportion, but its duration goes in the
inverse proportion. The time integral of the field
is independent of 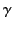 . As
. As
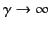 , the observer
at
, the observer
at 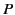 sees electric and magnetic fields that are indistinguishable
from the fields of a pulse of plane polarized radiation propagating in
the
sees electric and magnetic fields that are indistinguishable
from the fields of a pulse of plane polarized radiation propagating in
the 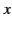 -direction. The direction of polarization is along the radius vector
pointing towards the particle's actual position at the time of observation.
-direction. The direction of polarization is along the radius vector
pointing towards the particle's actual position at the time of observation.



Next: Relativistic Particle Dynamics
Up: Relativity and Electromagnetism
Previous: Potential Due to a
Richard Fitzpatrick
2014-06-27
![]() , whose position vector at time
, whose position vector at time ![]() is
is ![]() , move with
uniform velocity
, move with
uniform velocity ![]() in a frame
in a frame ![]() whose
whose ![]() -axis has been chosen
in the direction of
-axis has been chosen
in the direction of ![]() . We require to find the field strengths
. We require to find the field strengths
![]() and
and ![]() at the event
at the event
![]() . Let
. Let ![]() be that frame
in standard configuration with
be that frame
in standard configuration with ![]() in which the charge is permanently at
rest. In
in which the charge is permanently at
rest. In ![]() , the field is given by
, the field is given by
![]() on the left-hand side, and the position 4-vector
on the left-hand side, and the position 4-vector
![]() and the scalar
and the scalar
![]() on the right-hand side. (We regard
on the right-hand side. (We regard ![]() as an invariant for all observers.)
To get a vanishing magnetic field in
as an invariant for all observers.)
To get a vanishing magnetic field in ![]() , we multiply on the right
by the 4-velocity
, we multiply on the right
by the 4-velocity
![]() , thus tentatively
arriving at the equation
, thus tentatively
arriving at the equation
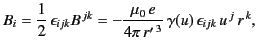
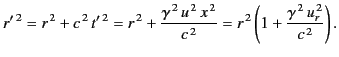
![]() , Equations (1835) and (1836) reduce to the
well-known Coulomb and Biot-Savart fields. However, at high
velocities,
, Equations (1835) and (1836) reduce to the
well-known Coulomb and Biot-Savart fields. However, at high
velocities,
![]() , the fields exhibit some interesting behavior.
The peak electric field, which occurs at the point of closest approach
of the charge to the observation point, becomes equal to
, the fields exhibit some interesting behavior.
The peak electric field, which occurs at the point of closest approach
of the charge to the observation point, becomes equal to ![]() times
its non-relativistic value. However, the duration of appreciable
field strength at the point
times
its non-relativistic value. However, the duration of appreciable
field strength at the point ![]() is decreased. A measure of the time
interval over which the field is appreciable is
is decreased. A measure of the time
interval over which the field is appreciable is