Transformation of Fields

The electromagnetic field tensor transforms according to the standard rule

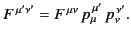$$F^{\,\mu'\nu'} = F^{\,\mu\nu} \,p_\mu^{\,\mu'} \,p_{\nu}^{\,\nu'}.$$ (1806)

This easily yields the celebrated rules for transforming electromagnetic fields:

$$E_\parallel' = E_\parallel,$$ (1807)

$$B_\parallel' = B_\parallel,$$ (1808)

$${\bf E}_\perp' = \gamma\,({\bf E}_\perp +{\bf v}\times{\bf B}),$$ (1809)

$${\bf B}_\perp' = \gamma\,({\bf B}_\perp-{\bf v}\times{\bf E}/c^2),$$ (1810)

where ${\bf v}$ is the relative velocity between the primed and unprimed frames, and the perpendicular and parallel directions are, respectively, perpendicular and parallel to ${\bf v}$ .

At this stage, we may conveniently note two important invariants of the electromagnetic field. They are

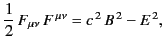$$\frac{1}{2}\, F_{\mu\nu} \,F^{\,\mu\nu} = c^{\,2} \,B^{\,2} - E^{\,2},$$ (1811)

and

$$\frac{1}{4} \,G_{\mu\nu} \,F^{\,\mu\nu} = c\,{\bf E} \cdot {\bf B}.$$ (1812)

The first of these quantities is a proper-scalar, and the second a pseudo-scalar.