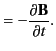Next: Transformation of Fields
Up: Relativity and Electromagnetism
Previous: Electromagnetic Field Tensor
We have seen that it is possible to write the components of
the electric and magnetic fields as the components of a proper-4-tensor.
Is it also possible to write the components of these fields as the components
of some pseudo-4-tensor? It is obvious that we cannot identify
the components of
the proper-3-vector 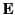 with any of the components of a
pseudo-tensor. However, we can represent the components of
with any of the components of a
pseudo-tensor. However, we can represent the components of 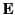 in terms of those of an antisymmetric pseudo-3-tensor
in terms of those of an antisymmetric pseudo-3-tensor 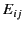 by writing
by writing
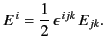 |
(1786) |
It is easily demonstrated that
![$\displaystyle E^{\,ij}=E_{ij} = \left(\begin{array}{ccc} 0& E_z & -E_y\\ [0.5ex] -E_z & 0 & E_x \\ [0.5ex] E_y & -E_x & 0 \end{array} \right),$](img3816.png) |
(1787) |
in a right-handed coordinate system.
Consider the dual electromagnetic field tensor,
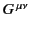 ,
which is defined
,
which is defined
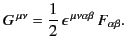 |
(1788) |
This tensor is clearly an antisymmetric pseudo-4-tensor. We have
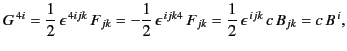 |
(1789) |
plus
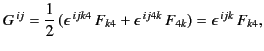 |
(1790) |
where use has been made of
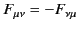 . The previous
expression yields
. The previous
expression yields
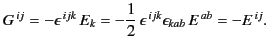 |
(1791) |
It follows that
or
![$\displaystyle G^{\mu\nu} = \left\lgroup \begin{array}{cccc} 0 & -E_z & +E_y & -...
...& 0& -c\,B_z\\ [0.5ex] +c\,B_x &+ c\,B_y &+c\,B_z & 0\end{array}\right \rgroup.$](img3827.png) |
(1794) |
The previous expression is, again, slightly misleading, because
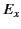 stands for the component
stands for the component 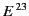 of the pseudo-3-tensor
of the pseudo-3-tensor 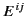 ,
and not for an element of the proper-3-vector
,
and not for an element of the proper-3-vector 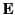 . Of course,
in this case,
. Of course,
in this case, 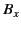 really does represent
the first element of the pseudo-3-vector
really does represent
the first element of the pseudo-3-vector
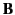 .
Note that the elements of
.
Note that the elements of
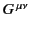 are obtained from those of
are obtained from those of
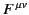 by making the transformation
by making the transformation
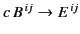 and
and
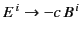 .
.
The covariant elements of the dual electromagnetic field tensor are
given by
or
![$\displaystyle G_{\mu\nu} = \left\lgroup \begin{array}{cccc} 0 & -E_z & +E_y & +...
...& 0& +c\,B_z\\ [0.5ex] -c\,B_x & -c\,B_y &-c\,B_z & 0\end{array}\right \rgroup.$](img3837.png) |
(1797) |
The elements of
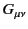 are obtained from those of
are obtained from those of
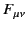 by making the transformation
by making the transformation
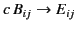 and
and
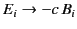 .
.
Let us now consider the two Maxwell equations
The first of these equations can be written
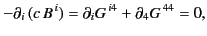 |
(1800) |
because
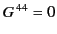 . The second equation takes the form
. The second equation takes the form
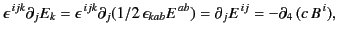 |
(1801) |
or
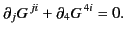 |
(1802) |
Equations (1802) and (1804) can be combined to give
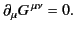 |
(1803) |
Thus, we conclude that Maxwell's equations for the electromagnetic fields
are equivalent to the following pair of 4-tensor equations:
It is obvious from the form of these equations that the laws of electromagnetism
are invariant under translations, rotations, special Lorentz transformations,
parity inversions, or any combination of these transformations.



Next: Transformation of Fields
Up: Relativity and Electromagnetism
Previous: Electromagnetic Field Tensor
Richard Fitzpatrick
2014-06-27
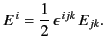
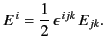
![$\displaystyle E^{\,ij}=E_{ij} = \left(\begin{array}{ccc} 0& E_z & -E_y\\ [0.5ex] -E_z & 0 & E_x \\ [0.5ex] E_y & -E_x & 0 \end{array} \right),$](img3816.png)
![]() ,
which is defined
,
which is defined
![$\displaystyle G^{\mu\nu} = \left\lgroup \begin{array}{cccc} 0 & -E_z & +E_y & -...
...& 0& -c\,B_z\\ [0.5ex] +c\,B_x &+ c\,B_y &+c\,B_z & 0\end{array}\right \rgroup.$](img3827.png)
![$\displaystyle G_{\mu\nu} = \left\lgroup \begin{array}{cccc} 0 & -E_z & +E_y & +...
...& 0& +c\,B_z\\ [0.5ex] -c\,B_x & -c\,B_y &-c\,B_z & 0\end{array}\right \rgroup.$](img3837.png)