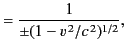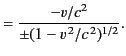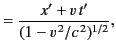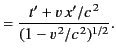Next: Transformation of Velocities
Up: Relativity and Electromagnetism
Previous: Relativity Principle
Lorentz Transformation
Consider two Cartesian frames
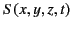 and
and
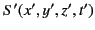 in
the standard configuration, in which
in
the standard configuration, in which  moves in the
moves in the  -direction
of
-direction
of  with uniform velocity
with uniform velocity  , and the corresponding axes of
, and the corresponding axes of
 and
and  remain parallel throughout the motion, having
coincided at
remain parallel throughout the motion, having
coincided at 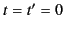 . It is assumed that the same units of distance and
time are adopted in both frames. Suppose that an event
(e.g., the flashing of a light-bulb, or the collision of
two point particles) has coordinates (
. It is assumed that the same units of distance and
time are adopted in both frames. Suppose that an event
(e.g., the flashing of a light-bulb, or the collision of
two point particles) has coordinates ( ,
, 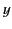 ,
,  ,
, 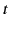 ) relative
to
) relative
to  , and (
, and (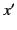 ,
, 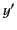 ,
, 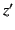 ,
, 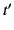 ) relative
to
) relative
to  . The ``common sense'' relationship between these two sets of
coordinates is given by the Galilean transformation:
. The ``common sense'' relationship between these two sets of
coordinates is given by the Galilean transformation:
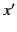 |
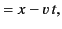 |
(1619) |
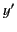 |
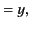 |
(1620) |
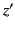 |
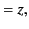 |
(1621) |
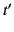 |
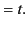 |
(1622) |
This transformation is tried and tested, and provides a very accurate
description of our everyday experience.
Nevertheless, it must be wrong. Consider a light wave that propagates
along the  -axis in
-axis in  with velocity
with velocity 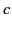 . According to the Galilean
transformation, the apparent speed of propagation in
. According to the Galilean
transformation, the apparent speed of propagation in  is
is
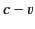 , which violates the relativity principle. Can we construct a
new transformation that makes the velocity of light invariant between
different inertial frames, in accordance with
the relativity principle, but reduces to the Galilean transformation
at low velocities, in accordance with our everyday experience?
, which violates the relativity principle. Can we construct a
new transformation that makes the velocity of light invariant between
different inertial frames, in accordance with
the relativity principle, but reduces to the Galilean transformation
at low velocities, in accordance with our everyday experience?
Consider an event 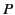 , and a neighboring event
, and a neighboring event 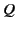 , whose coordinates
differ by
, whose coordinates
differ by 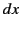 ,
, 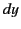 ,
, 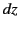 ,
, 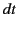 in
in  , and by
, and by
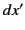 ,
, 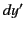 ,
, 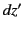 ,
, 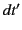 in
in  . Suppose that at the event
. Suppose that at the event 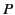 a flash of light is emitted, and that
a flash of light is emitted, and that 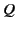 is an event in which some
particle in space is illuminated by the flash. In accordance with the
laws of light propagation, and the invariance of the velocity of
light between different inertial frames, an observer in
is an event in which some
particle in space is illuminated by the flash. In accordance with the
laws of light propagation, and the invariance of the velocity of
light between different inertial frames, an observer in  will
find that
will
find that
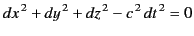 |
(1623) |
for 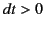 , and an observer in
, and an observer in  will find that
will find that
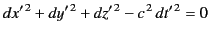 |
(1624) |
for  .
Any event near
.
Any event near  whose coordinates satisfy either (1625) or (1626)
is illuminated by the flash from
whose coordinates satisfy either (1625) or (1626)
is illuminated by the flash from  , and, therefore, its coordinates
must satisfy both (1625) and (1626).
Now, no matter what form the transformation between coordinates in the
two inertial frames takes, the transformation between differentials at
any fixed event
, and, therefore, its coordinates
must satisfy both (1625) and (1626).
Now, no matter what form the transformation between coordinates in the
two inertial frames takes, the transformation between differentials at
any fixed event 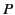 is linear and homogeneous. In other words, if
is linear and homogeneous. In other words, if
 |
(1625) |
where 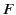 is a general function, then
is a general function, then
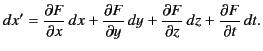 |
(1626) |
It follows that
where
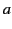 ,
,  ,
, 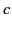 , et cetera, are functions of
, et cetera, are functions of  ,
, 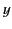 ,
,  , and
, and 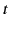 .
We know that the right-hand side of the previous expression vanishes for
all real values of the differentials that satisfy Equation (1625). It follows
that the right-hand side is a multiple of the quadratic in Equation (1625):
that is,
.
We know that the right-hand side of the previous expression vanishes for
all real values of the differentials that satisfy Equation (1625). It follows
that the right-hand side is a multiple of the quadratic in Equation (1625):
that is,
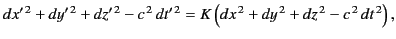 |
(1628) |
where 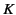 is a function of
is a function of  ,
, 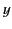 ,
,  , and
, and 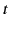 .
[We can prove this by substituting into Equation (1629) the following obvious
zeros of the quadratic in Equation (1625):
.
[We can prove this by substituting into Equation (1629) the following obvious
zeros of the quadratic in Equation (1625):
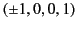 ,
,
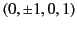 ,
,
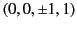 ,
,
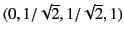 ,
,
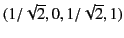 ,
,
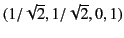 : and solving the resulting conditions
on the coefficients.]
Note that
: and solving the resulting conditions
on the coefficients.]
Note that 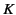 at
at 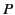 is also independent of the choice of standard coordinates
in
is also independent of the choice of standard coordinates
in  and
and  . Because the frames are Euclidian, the values of
. Because the frames are Euclidian, the values of
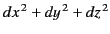 and
and
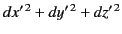 relevant to
relevant to 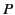 and
and 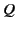 are independent of the choice of axes. Furthermore, the values of
are independent of the choice of axes. Furthermore, the values of
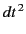 and
and 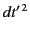 are independent of the choice of the origins
of time. Thus, without affecting the value of
are independent of the choice of the origins
of time. Thus, without affecting the value of 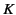 at
at 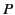 , we can
choose coordinates such that
, we can
choose coordinates such that
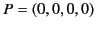 in both
in both  and
and  . Because the
orientations of the axes in
. Because the
orientations of the axes in  and
and  are, at present, arbitrary, and
because inertial frames are isotropic, the relation of
are, at present, arbitrary, and
because inertial frames are isotropic, the relation of  and
and
 relative to each other, to the event
relative to each other, to the event 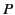 , and
to the locus of possible events
, and
to the locus of possible events 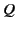 , is now completely
symmetric. Thus, we can write
, is now completely
symmetric. Thus, we can write
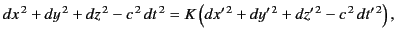 |
(1629) |
in addition to Equation (1630). It follows that 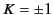 .
. 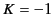 can be
dismissed immediately, because the intervals
can be
dismissed immediately, because the intervals
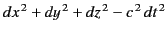 and
and
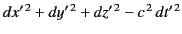 must coincide exactly when there is no motion of
must coincide exactly when there is no motion of  relative to
relative to  .
Thus,
.
Thus,
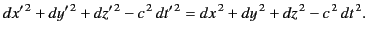 |
(1630) |
Equation (1632) implies that the transformation equations between primed
and unprimed coordinates must be linear. The proof of this statement is
postponed until Section 12.7.
The linearity of the transformation allows the coordinate axes in the
two frames to be orientated so as to give the standard configuration
mentioned previously. Consider a fixed plane in  with the equation
with the equation
 . In
. In  , this becomes (say)
, this becomes (say)
 ,
which represents a moving plane unless
,
which represents a moving plane unless
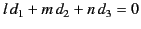 .
That is, unless the normal vector to the plane in
.
That is, unless the normal vector to the plane in  ,
, 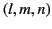 ,
is perpendicular to the vector
,
is perpendicular to the vector
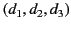 . All such planes
intersect in lines that are fixed in both
. All such planes
intersect in lines that are fixed in both  and
and  , and that are
parallel to the vector
, and that are
parallel to the vector
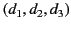 in
in  . These lines must correspond
to the direction of relative motion of the frames. By symmetry, two such
planes which are orthogonal in
. These lines must correspond
to the direction of relative motion of the frames. By symmetry, two such
planes which are orthogonal in  must also be orthogonal in
must also be orthogonal in  . This
allows the choice of two common coordinate planes.
. This
allows the choice of two common coordinate planes.
Under a linear transformation, the finite coordinate differences satisfy the
same transformation equations as the differentials. It follows from
Equation (1632),
assuming that the events 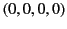 coincide in both frames,
that for any event with
coordinates
coincide in both frames,
that for any event with
coordinates
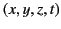 in
in  and
and
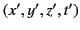 in
in  , the following relation holds:
, the following relation holds:
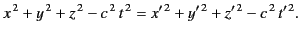 |
(1631) |
By hypothesis, the coordinate planes 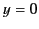 and
and 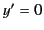 coincide
permanently. Thus,
coincide
permanently. Thus, 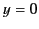 must imply
must imply 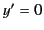 , which suggests that
, which suggests that
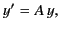 |
(1632) |
where  is a constant. We can reverse the directions of the
is a constant. We can reverse the directions of the
 - and
- and  -axes in
-axes in  and
and  , which has the effect of interchanging the
roles of these frames. This procedure does not affect Equation (1634), but
by symmetry we also have
, which has the effect of interchanging the
roles of these frames. This procedure does not affect Equation (1634), but
by symmetry we also have
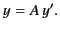 |
(1633) |
It is clear that 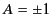 . The negative sign can again be dismissed,
because
. The negative sign can again be dismissed,
because 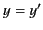 when there is no motion between
when there is no motion between  and
and  . The argument
for
. The argument
for  is similar. Thus, we have
is similar. Thus, we have
as in the Galilean transformation.
Equations (1633), (1636) and (1637) yield
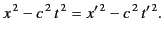 |
(1636) |
Because 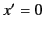 must imply
must imply 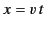 , we can write
, we can write
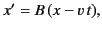 |
(1637) |
where 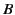 is a constant (possibly depending on
is a constant (possibly depending on  ).
It follows from the previous two equations that
).
It follows from the previous two equations that
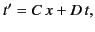 |
(1638) |
where  and
and 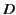 are constants (possibly depending on
are constants (possibly depending on  ). Substituting
Equations (1639) and (1640) into Equation (1638), and comparing the coefficients of
). Substituting
Equations (1639) and (1640) into Equation (1638), and comparing the coefficients of
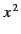 ,
, 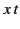 , and
, and  , we obtain
, we obtain
We must choose the positive sign in order to ensure that
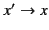 as
as
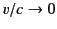 . Thus, collecting our results, the transformation
between coordinates in
. Thus, collecting our results, the transformation
between coordinates in  and
and  is given by
is given by
This is the famous Lorentz transformation. It ensures that
the velocity of light is invariant between different inertial
frames, and also reduces to the more familiar Galilean transform
in the limit 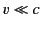 . We can solve Equations (1643)-(1646)
for
. We can solve Equations (1643)-(1646)
for  ,
, 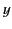 ,
,  , and
, and 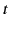 , to obtain the inverse Lorentz
transformation:
, to obtain the inverse Lorentz
transformation:
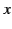 |
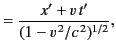 |
(1645) |
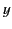 |
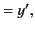 |
(1646) |
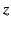 |
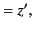 |
(1647) |
 |
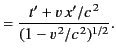 |
(1648) |
Not surprisingly, the inverse transformation is equivalent to a Lorentz transformation in
which the velocity of the moving frame is 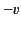 along the
along the  -axis, instead
of
-axis, instead
of 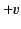 .
.



Next: Transformation of Velocities
Up: Relativity and Electromagnetism
Previous: Relativity Principle
Richard Fitzpatrick
2014-06-27
![]() , and a neighboring event
, and a neighboring event ![]() , whose coordinates
differ by
, whose coordinates
differ by ![]() ,
, ![]() ,
, ![]() ,
, ![]() in
in ![]() , and by
, and by
![]() ,
, ![]() ,
, ![]() ,
, ![]() in
in ![]() . Suppose that at the event
. Suppose that at the event ![]() a flash of light is emitted, and that
a flash of light is emitted, and that ![]() is an event in which some
particle in space is illuminated by the flash. In accordance with the
laws of light propagation, and the invariance of the velocity of
light between different inertial frames, an observer in
is an event in which some
particle in space is illuminated by the flash. In accordance with the
laws of light propagation, and the invariance of the velocity of
light between different inertial frames, an observer in ![]() will
find that
will
find that
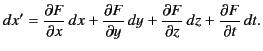
![]() with the equation
with the equation
![]() . In
. In ![]() , this becomes (say)
, this becomes (say)
![]() ,
which represents a moving plane unless
,
which represents a moving plane unless
![]() .
That is, unless the normal vector to the plane in
.
That is, unless the normal vector to the plane in ![]() ,
, ![]() ,
is perpendicular to the vector
,
is perpendicular to the vector
![]() . All such planes
intersect in lines that are fixed in both
. All such planes
intersect in lines that are fixed in both ![]() and
and ![]() , and that are
parallel to the vector
, and that are
parallel to the vector
![]() in
in ![]() . These lines must correspond
to the direction of relative motion of the frames. By symmetry, two such
planes which are orthogonal in
. These lines must correspond
to the direction of relative motion of the frames. By symmetry, two such
planes which are orthogonal in ![]() must also be orthogonal in
must also be orthogonal in ![]() . This
allows the choice of two common coordinate planes.
. This
allows the choice of two common coordinate planes.
![]() coincide in both frames,
that for any event with
coordinates
coincide in both frames,
that for any event with
coordinates
![]() in
in ![]() and
and
![]() in
in ![]() , the following relation holds:
, the following relation holds: