


Next: Lorentz Transformation
Up: Relativity and Electromagnetism
Previous: Introduction
Physical phenomena are conventionally described relative to some
frame of reference that allows us to define
fundamental quantities such
as position and time. Of course,
there are very many different ways
of choosing a reference frame, but it is generally convenient to
restrict our choice to the set of rigid inertial frames.
A classical rigid reference frame is the imagined extension of
a rigid body. For instance, the Earth determines a rigid frame
throughout all space, consisting of all those points that
remain rigidly at rest relative to the Earth, and to one another.
We can associate an orthogonal Cartesian coordinate system 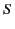 with
such a frame by choosing three mutually orthogonal planes within it,
and measuring
with
such a frame by choosing three mutually orthogonal planes within it,
and measuring 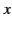 ,
, 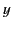 , and
, and 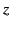 as perpendicular distances from these planes. A time
coordinate must also be defined, in order that the system can be used to
specify events. A rigid frame, endowed with such properties, is called
a Cartesian frame. The description given previously presupposes that the
underlying
geometry of space is Euclidian, which is reasonable provided that
gravitational effects are negligible (as we shall assume to be the case).
An inertial frame is a Cartesian frame in which free particles
move without acceleration, in accordance with Newton's first law of motion.
There are an infinite number of different inertial frames, moving with
some
constant velocity with respect to one another.
as perpendicular distances from these planes. A time
coordinate must also be defined, in order that the system can be used to
specify events. A rigid frame, endowed with such properties, is called
a Cartesian frame. The description given previously presupposes that the
underlying
geometry of space is Euclidian, which is reasonable provided that
gravitational effects are negligible (as we shall assume to be the case).
An inertial frame is a Cartesian frame in which free particles
move without acceleration, in accordance with Newton's first law of motion.
There are an infinite number of different inertial frames, moving with
some
constant velocity with respect to one another.
The key to understanding
special relativity is Einstein's Relativity Principle,
which states that:
All inertial frames are totally equivalent for the performance
of all physical experiments.
In other words, it is impossible to perform a physical experiment that
differentiates in any fundamental sense
between different inertial frames. By definition, Newton's laws
of motion take the same form in all inertial frames. Einstein
generalized this result in his special theory of relativity by
asserting that all
laws of physics take the same form in all inertial frames.
Consider a wave-like disturbance.
In general, such a disturbance propagates at a fixed speed
with respect to the medium in which the disturbance takes place.
For instance, sound waves (at STP) propagate at 343 meters per
second with respect to air. So, in the inertial frame in which
air is stationary, sound waves appear to propagate at
343 meters per second.
Sound waves appear to propagate at a different speed in any
inertial frame that is moving
with respect to the air.
However, this does not violate the relativity principle, because if the air
were stationary in the second frame then sound waves would appear to
propagate at 343 meters per second in that frame as well. In other words,
exactly the same experiment (e.g.,
the determination of the speed of sound relative to
stationary air)
performed in two different inertial frames
of reference yields exactly the same result, in accordance with the relativity
principle.
Consider, now, a wave-like disturbance that is self-regenerating, and
does not require a medium through which to propagate. The most well-known
example of such a disturbance is a light wave. Another example is
a gravity wave. According to electromagnetic theory, the speed of propagation
of a light wave through a vacuum is
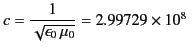 meters per second meters per second |
(1618) |
where
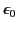 and
and 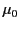 are physical constants that can
be evaluated by performing two simple experiments which
involve measuring the
forces of attraction between two fixed changes and two fixed parallel
current carrying wires. According to the relativity principle, these
experiments must yield the same values for
are physical constants that can
be evaluated by performing two simple experiments which
involve measuring the
forces of attraction between two fixed changes and two fixed parallel
current carrying wires. According to the relativity principle, these
experiments must yield the same values for
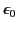 and
and 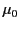 in all
inertial frames. Thus, the speed of light must be the same in all
inertial frames. In fact, any disturbance that does not require
a medium to propagate through must appear to travel at the same speed in
all inertial frames, otherwise we could differentiate inertial frames
using the apparent propagation speed of the disturbance, which
would violate the
relativity principle.
in all
inertial frames. Thus, the speed of light must be the same in all
inertial frames. In fact, any disturbance that does not require
a medium to propagate through must appear to travel at the same speed in
all inertial frames, otherwise we could differentiate inertial frames
using the apparent propagation speed of the disturbance, which
would violate the
relativity principle.



Next: Lorentz Transformation
Up: Relativity and Electromagnetism
Previous: Introduction
Richard Fitzpatrick
2014-06-27
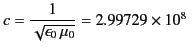 meters per second
meters per second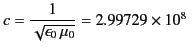 meters per second
meters per second