


Next: Rayleigh scattering
Up: Electromagnetic radiation
Previous: Electric dipole radiation
Consider a plane electromagnetic wave of angular frequency 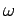 interacting with a free electron of mass
interacting with a free electron of mass 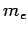 and charge
and charge 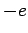 . Suppose that
the wave is polarized such that its associated electric field is parallel
to the
. Suppose that
the wave is polarized such that its associated electric field is parallel
to the  -axis: i.e.,
-axis: i.e.,
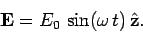 |
(1120) |
Recall, from Sect. 4.7, that as long as the electron remains non-relativistic, the force exerted on it by the electromagnetic wave comes
predominantly from the associated electric field. Hence, the electron's equation of
motion can be written
 |
(1121) |
which can be solved to give
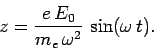 |
(1122) |
So, in response to the wave, the electron oscillates backward and forward in the direction of the
wave electric field. It follows that the electron can be thought of as a sort of
oscillating electric dipole, with dipole moment
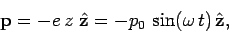 |
(1123) |
where
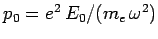 . (For the moment, let us not worry about the
positively charged component of the dipole.) Now, we know that an
oscillating electric dipole emits electromagnetic radiation. Hence, it
follows that a free electron placed in the path of a plane
electromagnetic wave will radiate. To be more exact, the electron
scatters electromagnetic radiation from the wave, since the
radiation emitted by the electron is not necessarily in the same direction
as the wave, and any energy radiated by the electron is ultimately extracted
from the wave. This type of scattering is called Thompson scattering.
. (For the moment, let us not worry about the
positively charged component of the dipole.) Now, we know that an
oscillating electric dipole emits electromagnetic radiation. Hence, it
follows that a free electron placed in the path of a plane
electromagnetic wave will radiate. To be more exact, the electron
scatters electromagnetic radiation from the wave, since the
radiation emitted by the electron is not necessarily in the same direction
as the wave, and any energy radiated by the electron is ultimately extracted
from the wave. This type of scattering is called Thompson scattering.
It follows from Eq. (1119) that the differential power scattered
from a plane electromagnetic wave
by a free electron into solid angle
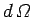 takes the form
takes the form
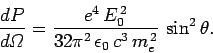 |
(1124) |
Now, the mean energy flux of the incident electromagnetic wave is written
 |
(1125) |
It is helpful to introduce a quantity called the differential scattering cross-section. This is defined
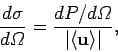 |
(1126) |
and has units of area over solid angle. Somewhat figuratively, we can think
of the electron as offering a target of area
 to the
incident wave. Any wave energy which falls on this target is scattered into
the solid angle
to the
incident wave. Any wave energy which falls on this target is scattered into
the solid angle  . Likewise, we can also define the total scattering cross-section,
. Likewise, we can also define the total scattering cross-section,
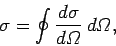 |
(1127) |
which has units of area. Again, the electron effectively offers a target of
area 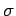 to the incident wave. Any wave energy which falls on this
target is scattered in some direction or other.
It follows from Eqs. (1124) and (1125) that the differential
scattering cross-section for Thompson scattering is
to the incident wave. Any wave energy which falls on this
target is scattered in some direction or other.
It follows from Eqs. (1124) and (1125) that the differential
scattering cross-section for Thompson scattering is
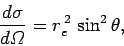 |
(1128) |
where the characteristic length
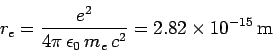 |
(1129) |
is called the classical electron radius. An electron effectively acts
like it has a spatial extent 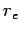 as far as its iteration with electromagnetic
radiation is concerned. As is easily demonstrated, the
total Thompson scattering cross-section is
as far as its iteration with electromagnetic
radiation is concerned. As is easily demonstrated, the
total Thompson scattering cross-section is
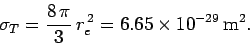 |
(1130) |
Note that both the differential and the total Thompson scattering cross-sections
are completely independent of the frequency (or wave-length) of the incident
radiation.
A scattering cross-section of
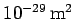 does not sound like much. Nevertheless, Thompson scattering is one of the most important types
of scattering in the Universe. Consider the Sun. It turns out that the
mean mass density of the Sun is similar to that of water: i.e.,
about
does not sound like much. Nevertheless, Thompson scattering is one of the most important types
of scattering in the Universe. Consider the Sun. It turns out that the
mean mass density of the Sun is similar to that of water: i.e.,
about
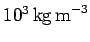 . Hence, assuming that
the Sun is made up predomintely of ionized hydrogen, the mean number density of electrons in the Sun (which, of course, is the same as
the number density of protons) is approximately
. Hence, assuming that
the Sun is made up predomintely of ionized hydrogen, the mean number density of electrons in the Sun (which, of course, is the same as
the number density of protons) is approximately
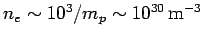 , where
, where
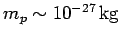 is the mass of a proton.
Let us consider how far, on average, a photon in the Sun travels before
being scattered by free electrons. If we think of an individual photon
as sweeping out a cylinder of cross-sectional area
is the mass of a proton.
Let us consider how far, on average, a photon in the Sun travels before
being scattered by free electrons. If we think of an individual photon
as sweeping out a cylinder of cross-sectional area 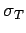 , then the photon will travel an average length
, then the photon will travel an average length  , such that a cylinder of area
, such that a cylinder of area 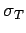 and length
and length  contains about one free electron, before
being scattered. Hence,
contains about one free electron, before
being scattered. Hence,
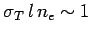 , or
, or
 |
(1131) |
Given that the radius of the Sun is approximately 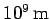 , it is
clear that solar photons are very strongly scattered by free electrons.
In fact, it can easily be demonstrated that it takes a photon emitted in the solar
core many thousands of years to fight its way to the surface
because of Thompson scattering.
, it is
clear that solar photons are very strongly scattered by free electrons.
In fact, it can easily be demonstrated that it takes a photon emitted in the solar
core many thousands of years to fight its way to the surface
because of Thompson scattering.
After the ``Big Bang'', when the Universe was very hot, it consisted
predominately of ionized hydrogen (and dark matter), and was consequently
opaque to electromagnetic radiation, due to Thompson scattering. However,
as the Universe expanded, it also cooled, and eventually became sufficiently
cold (when the mean temperature was about
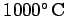 ) for any free protons and electrons to combine to form molecular
hydrogen. It turns out that molecular hydrogen does not scatter radiation
anything like as effectively as free electrons (see the next section). Hence, as soon as the
Universe became filled with molecular hydrogen, it effectively became
transparent to radiation. Indeed, the so-called cosmic microwave background is the remnant of radiation which was last scattered
when the Universe was filled with ionized hydrogen (i.e., when it was about
) for any free protons and electrons to combine to form molecular
hydrogen. It turns out that molecular hydrogen does not scatter radiation
anything like as effectively as free electrons (see the next section). Hence, as soon as the
Universe became filled with molecular hydrogen, it effectively became
transparent to radiation. Indeed, the so-called cosmic microwave background is the remnant of radiation which was last scattered
when the Universe was filled with ionized hydrogen (i.e., when it was about
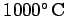 ). Astronomers can gain a great deal of information
about the conditions in the early Universe by studying this radiation.
). Astronomers can gain a great deal of information
about the conditions in the early Universe by studying this radiation.
Incidentally, it is clear from Eqs. (1129) and (1130) that the scattering cross-section of a free particle of charge 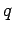 and mass
and mass 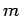 is proportional to
is proportional to
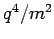 . It follows that the scattering of electromagnetic radiation by free electrons is generally very much
stronger than the scattering by free protons (assuming that the
number densities of both species are similar).
. It follows that the scattering of electromagnetic radiation by free electrons is generally very much
stronger than the scattering by free protons (assuming that the
number densities of both species are similar).



Next: Rayleigh scattering
Up: Electromagnetic radiation
Previous: Electric dipole radiation
Richard Fitzpatrick
2006-02-02
![]() takes the form
takes the form
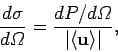
![]() does not sound like much. Nevertheless, Thompson scattering is one of the most important types
of scattering in the Universe. Consider the Sun. It turns out that the
mean mass density of the Sun is similar to that of water: i.e.,
about
does not sound like much. Nevertheless, Thompson scattering is one of the most important types
of scattering in the Universe. Consider the Sun. It turns out that the
mean mass density of the Sun is similar to that of water: i.e.,
about
![]() . Hence, assuming that
the Sun is made up predomintely of ionized hydrogen, the mean number density of electrons in the Sun (which, of course, is the same as
the number density of protons) is approximately
. Hence, assuming that
the Sun is made up predomintely of ionized hydrogen, the mean number density of electrons in the Sun (which, of course, is the same as
the number density of protons) is approximately
![]() , where
, where
![]() is the mass of a proton.
Let us consider how far, on average, a photon in the Sun travels before
being scattered by free electrons. If we think of an individual photon
as sweeping out a cylinder of cross-sectional area
is the mass of a proton.
Let us consider how far, on average, a photon in the Sun travels before
being scattered by free electrons. If we think of an individual photon
as sweeping out a cylinder of cross-sectional area ![]() , then the photon will travel an average length
, then the photon will travel an average length ![]() , such that a cylinder of area
, such that a cylinder of area ![]() and length
and length ![]() contains about one free electron, before
being scattered. Hence,
contains about one free electron, before
being scattered. Hence,
![]() , or
, or
![]() ) for any free protons and electrons to combine to form molecular
hydrogen. It turns out that molecular hydrogen does not scatter radiation
anything like as effectively as free electrons (see the next section). Hence, as soon as the
Universe became filled with molecular hydrogen, it effectively became
transparent to radiation. Indeed, the so-called cosmic microwave background is the remnant of radiation which was last scattered
when the Universe was filled with ionized hydrogen (i.e., when it was about
) for any free protons and electrons to combine to form molecular
hydrogen. It turns out that molecular hydrogen does not scatter radiation
anything like as effectively as free electrons (see the next section). Hence, as soon as the
Universe became filled with molecular hydrogen, it effectively became
transparent to radiation. Indeed, the so-called cosmic microwave background is the remnant of radiation which was last scattered
when the Universe was filled with ionized hydrogen (i.e., when it was about
![]() ). Astronomers can gain a great deal of information
about the conditions in the early Universe by studying this radiation.
). Astronomers can gain a great deal of information
about the conditions in the early Universe by studying this radiation.
![]() and mass
and mass ![]() is proportional to
is proportional to
![]() . It follows that the scattering of electromagnetic radiation by free electrons is generally very much
stronger than the scattering by free protons (assuming that the
number densities of both species are similar).
. It follows that the scattering of electromagnetic radiation by free electrons is generally very much
stronger than the scattering by free protons (assuming that the
number densities of both species are similar).