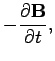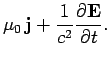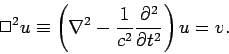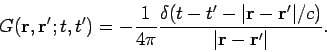Next: Electrostatics
Up: Time-dependent Maxwell's equations
Previous: Retarded fields
Summary
This marks the end of our theoretical investigation of Maxwell's equations. Let us now summarize
what we have learned so far. The field equations which govern electric and magnetic fields
are written:
These equations can be integrated to give
Equations (557) and (558) are automatically satisfied by writing
This prescription is not unique (there are many choices of 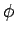 and
and 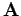 which
generate the same fields) but we can make it unique by adopting the following conventions:
which
generate the same fields) but we can make it unique by adopting the following conventions:
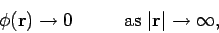 |
(566) |
and
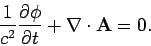 |
(567) |
Equations (556) and (559) reduce to
These are driven wave equations of the general form
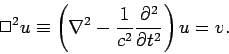 |
(570) |
The Green's function for this equation which satisfies the boundary conditions and is
consistent with causality is
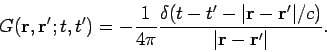 |
(571) |
Thus, the solutions to Eqs. (568) and (569) are
where
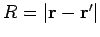 , and
, and
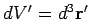 , with
, with
![$[A] \equiv A({\bf r}', t-R/c)$](img1231.png) . These solutions can be combined with
Eqs. (564) and (565) to give
. These solutions can be combined with
Eqs. (564) and (565) to give
Equations (556)-(575) constitute the complete theory of classical electromagnetism.
We can express the same information in terms of field equations [Eqs. (556)-(559)],
integrated field equations [Eqs. (560)-(563)], retarded electromagnetic
potentials [Eqs. (572) and (573)], and retarded electromagnetic
fields [Eqs. (574) and (575)]. Let us now consider the applications of this theory.



Next: Electrostatics
Up: Time-dependent Maxwell's equations
Previous: Retarded fields
Richard Fitzpatrick
2006-02-02