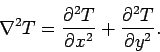Next: Curl
Up: Vectors
Previous: Divergence
So far we have encountered
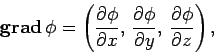 |
(131) |
which is a vector field formed from a scalar field, and
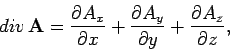 |
(132) |
which is a scalar field formed from a vector field. There are two ways in which
we can combine 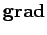 and div. We can either form the vector field
and div. We can either form the vector field
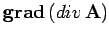 or the scalar field
or the scalar field
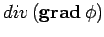 .
The former is not particularly interesting, but the scalar field
.
The former is not particularly interesting, but the scalar field
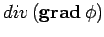 turns up in a great many physics problems, and is,
therefore, worthy of discussion.
turns up in a great many physics problems, and is,
therefore, worthy of discussion.
Let us introduce the heat flow vector 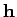 , which is the rate of flow of heat
energy per unit area across a surface perpendicular to the direction of
, which is the rate of flow of heat
energy per unit area across a surface perpendicular to the direction of 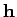 .
In many substances, heat flows directly down the temperature gradient, so that we
can write
.
In many substances, heat flows directly down the temperature gradient, so that we
can write
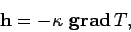 |
(133) |
where 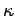 is the thermal conductivity. The net rate of heat flow
is the thermal conductivity. The net rate of heat flow
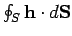 out of some closed surface
out of some closed surface  must be equal
to the rate of decrease of heat energy in the volume
must be equal
to the rate of decrease of heat energy in the volume  enclosed by
enclosed by  .
Thus, we can write
.
Thus, we can write
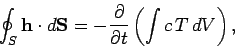 |
(134) |
where 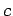 is the specific heat. It follows from the divergence theorem that
is the specific heat. It follows from the divergence theorem that
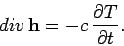 |
(135) |
Taking the divergence of both sides of Eq. (133), and making use of Eq. (135),
we obtain
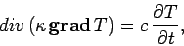 |
(136) |
or
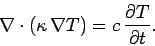 |
(137) |
If 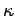 is constant then the above equation can be written
is constant then the above equation can be written
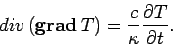 |
(138) |
The scalar field
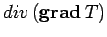 takes the form
takes the form
Here, the scalar differential operator
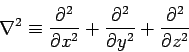 |
(140) |
is called the Laplacian. The Laplacian is a good scalar operator
(i.e., it is coordinate independent) because it is formed from a
combination of div
(another good scalar operator) and 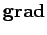 (a good vector
operator).
(a good vector
operator).
What is the physical significance of the Laplacian? In one dimension,
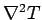 reduces to
reduces to
 .
Now,
.
Now,
 is positive if
is positive if 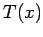 is
concave (from above) and negative if it is convex. So, if
is
concave (from above) and negative if it is convex. So, if 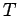 is less than the
average of
is less than the
average of 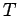 in its surroundings then
in its surroundings then 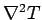 is positive, and vice
versa.
is positive, and vice
versa.
In two dimensions,
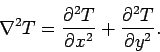 |
(141) |
Consider a local minimum of the temperature.
At the minimum, the slope of 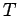 increases in all directions, so
increases in all directions, so 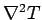 is
positive. Likewise,
is
positive. Likewise, 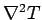 is negative at
a local maximum.
Consider, now, a steep-sided valley in
is negative at
a local maximum.
Consider, now, a steep-sided valley in 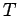 . Suppose that the bottom of the
valley runs parallel to the
. Suppose that the bottom of the
valley runs parallel to the 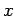 -axis.
At the bottom of the
valley
-axis.
At the bottom of the
valley
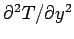 is large and positive, whereas
is large and positive, whereas
 is small and may even be negative. Thus,
is small and may even be negative. Thus, 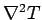 is positive, and this is associated with
is positive, and this is associated with 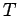 being less than the average local
value.
being less than the average local
value.
Let us now return to the heat conduction problem:
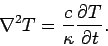 |
(142) |
It is clear that if 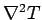 is positive then
is positive then 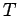 is locally less than the
average value, so
is locally less than the
average value, so
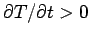 : i.e., the region heats up.
Likewise, if
: i.e., the region heats up.
Likewise, if 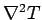 is negative then
is negative then 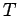 is locally greater than the average
value, and heat flows out of the region: i.e.,
is locally greater than the average
value, and heat flows out of the region: i.e.,
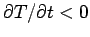 . Thus,
the above heat conduction equation makes physical sense.
. Thus,
the above heat conduction equation makes physical sense.



Next: Curl
Up: Vectors
Previous: Divergence
Richard Fitzpatrick
2006-02-02
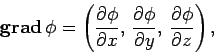
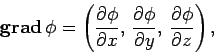
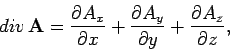
![]() , which is the rate of flow of heat
energy per unit area across a surface perpendicular to the direction of
, which is the rate of flow of heat
energy per unit area across a surface perpendicular to the direction of ![]() .
In many substances, heat flows directly down the temperature gradient, so that we
can write
.
In many substances, heat flows directly down the temperature gradient, so that we
can write
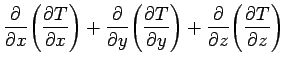
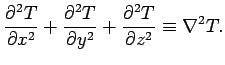
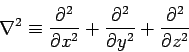
![]() reduces to
reduces to
![]() .
Now,
.
Now,
![]() is positive if
is positive if ![]() is
concave (from above) and negative if it is convex. So, if
is
concave (from above) and negative if it is convex. So, if ![]() is less than the
average of
is less than the
average of ![]() in its surroundings then
in its surroundings then ![]() is positive, and vice
versa.
is positive, and vice
versa.