


Next: The Laplacian
Up: Vectors
Previous: Gradient
Let us start with a vector field 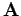 . Consider
. Consider
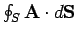 over some closed surface
over some closed surface  , where
, where 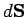 denotes an outward
pointing surface element. This surface integral is usually called the
flux of
denotes an outward
pointing surface element. This surface integral is usually called the
flux of 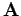 out of
out of  . If
. If 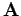 is the velocity of some fluid,
then
is the velocity of some fluid,
then
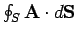 is the rate of flow of material out of
is the rate of flow of material out of  .
.
If 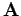 is constant in space then it is easily demonstrated that the net
flux out of
is constant in space then it is easily demonstrated that the net
flux out of  is zero,
is zero,
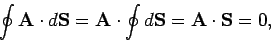 |
(119) |
since the vector area 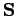 of a closed surface is zero.
of a closed surface is zero.
Figure 18:
 |
Suppose, now, that 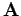 is not uniform in space. Consider a very small
rectangular volume over which
is not uniform in space. Consider a very small
rectangular volume over which  hardly varies. The contribution to
hardly varies. The contribution to
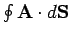 from the two faces normal to the
from the two faces normal to the 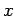 -axis is
-axis is
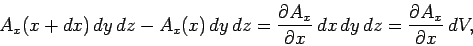 |
(120) |
where
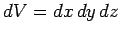 is the volume element (see Fig. 18).
There are analogous contributions
from the sides normal to the
is the volume element (see Fig. 18).
There are analogous contributions
from the sides normal to the 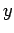 - and
- and 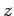 -axes, so the total of all the contributions
is
-axes, so the total of all the contributions
is
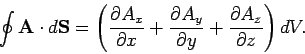 |
(121) |
The divergence of a vector field is defined
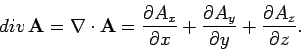 |
(122) |
Divergence is a good scalar (i.e., it is coordinate
independent),
since it is the dot product of
the vector operator 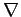 with
with 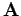 . The formal definition of
. The formal definition of
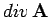 is
is
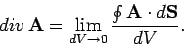 |
(123) |
This definition is independent of the shape of the infinitesimal volume
element.
Figure 19:
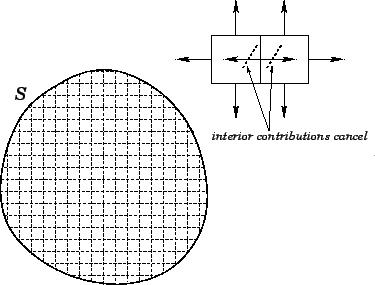 |
One of the most important results in vector field theory is the so-called
divergence theorem or Gauss' theorem. This states that for any volume
 surrounded by a closed surface
surrounded by a closed surface  ,
,
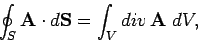 |
(124) |
where 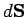 is an outward pointing volume element.
The proof is very
straightforward. We divide up the volume into lots of very small cubes, and
sum
is an outward pointing volume element.
The proof is very
straightforward. We divide up the volume into lots of very small cubes, and
sum
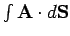 over all of the surfaces. The contributions
from the interior surfaces cancel out, leaving just the contribution from the outer
surface (see Fig. 19). We can use Eq. (121) for each cube individually. This tells us that
the summation is equivalent to
over all of the surfaces. The contributions
from the interior surfaces cancel out, leaving just the contribution from the outer
surface (see Fig. 19). We can use Eq. (121) for each cube individually. This tells us that
the summation is equivalent to
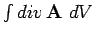 over the whole
volume. Thus, the integral of
over the whole
volume. Thus, the integral of
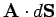 over the outer surface is
equal to the integral of
over the outer surface is
equal to the integral of
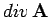 over the whole volume, which
proves the divergence theorem.
over the whole volume, which
proves the divergence theorem.
Now, for a vector field with
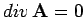 ,
,
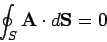 |
(125) |
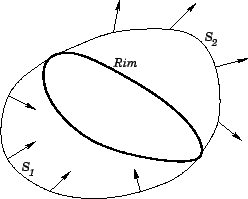
for any closed surface  . So, for two surfaces on the same rim (see Fig. 20),
. So, for two surfaces on the same rim (see Fig. 20),
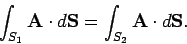 |
(126) |
Thus, if
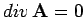 then the surface integral depends on the rim but
not the nature of the surface which spans it.
On the other hand, if
then the surface integral depends on the rim but
not the nature of the surface which spans it.
On the other hand, if
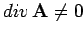 then the integral
depends on both the rim and the surface.
then the integral
depends on both the rim and the surface.
Figure 20:
 |
Consider an incompressible fluid whose velocity field is 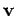 . It is clear that
. It is clear that
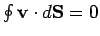 for any closed surface, since what flows into the
surface must flow out again. Thus, according to the divergence theorem,
for any closed surface, since what flows into the
surface must flow out again. Thus, according to the divergence theorem,
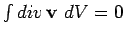 for any volume. The only way in which this is
possible is if
for any volume. The only way in which this is
possible is if
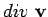 is everywhere zero. Thus, the velocity components
of an incompressible fluid satisfy the following differential relation:
is everywhere zero. Thus, the velocity components
of an incompressible fluid satisfy the following differential relation:
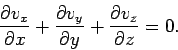 |
(127) |
Consider, now, a compressible fluid of density 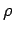 and velocity
and velocity 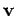 .
The surface integral
.
The surface integral
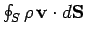 is the net rate of
mass flow out of the closed surface
is the net rate of
mass flow out of the closed surface  . This must be equal to the rate of
decrease of mass inside the volume
. This must be equal to the rate of
decrease of mass inside the volume  enclosed by
enclosed by  , which is written
, which is written
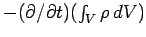 . Thus,
. Thus,
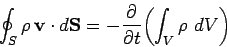 |
(128) |
for any volume. It follows from the divergence theorem that
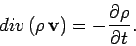 |
(129) |
This is called the equation of continuity of the fluid, since it ensures that
fluid is neither created nor destroyed as it flows from place to place.
If 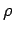 is constant then the equation of continuity reduces to the
previous incompressible
result,
is constant then the equation of continuity reduces to the
previous incompressible
result,
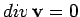 .
.
Figure 21:
 |
It is sometimes helpful to represent a vector field 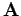 by lines of force
or field-lines.
The direction of a line of force at any point is the same as the direction of
by lines of force
or field-lines.
The direction of a line of force at any point is the same as the direction of
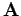 . The density of lines (i.e., the number of lines crossing a unit surface
perpendicular to
. The density of lines (i.e., the number of lines crossing a unit surface
perpendicular to 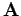 ) is equal to
) is equal to 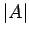 .
For instance, in Fig. 21,
.
For instance, in Fig. 21, 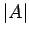 is larger at point 1 than at point 2. The number of lines
crossing a surface element
is larger at point 1 than at point 2. The number of lines
crossing a surface element 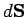 is
is
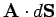 . So, the
net number of lines leaving a closed surface is
. So, the
net number of lines leaving a closed surface is
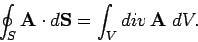 |
(130) |
If
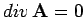 then there is no net flux of lines out of any surface.
Such a field is
called a solenoidal vector field. The simplest example of a solenoidal vector
field is one in which the lines of force all form closed loops.
then there is no net flux of lines out of any surface.
Such a field is
called a solenoidal vector field. The simplest example of a solenoidal vector
field is one in which the lines of force all form closed loops.



Next: The Laplacian
Up: Vectors
Previous: Gradient
Richard Fitzpatrick
2006-02-02
![]() is constant in space then it is easily demonstrated that the net
flux out of
is constant in space then it is easily demonstrated that the net
flux out of ![]() is zero,
is zero,
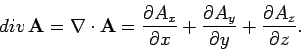
![]() ,
,
![]() . It is clear that
. It is clear that
![]() for any closed surface, since what flows into the
surface must flow out again. Thus, according to the divergence theorem,
for any closed surface, since what flows into the
surface must flow out again. Thus, according to the divergence theorem,
![]() for any volume. The only way in which this is
possible is if
for any volume. The only way in which this is
possible is if
![]() is everywhere zero. Thus, the velocity components
of an incompressible fluid satisfy the following differential relation:
is everywhere zero. Thus, the velocity components
of an incompressible fluid satisfy the following differential relation:
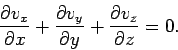
![]() and velocity
and velocity ![]() .
The surface integral
.
The surface integral
![]() is the net rate of
mass flow out of the closed surface
is the net rate of
mass flow out of the closed surface ![]() . This must be equal to the rate of
decrease of mass inside the volume
. This must be equal to the rate of
decrease of mass inside the volume ![]() enclosed by
enclosed by ![]() , which is written
, which is written
![]() . Thus,
. Thus,