


Next: Angular distribution of radiation
Up: Relativity and electromagnetism
Previous: The Larmor formula
Radiation losses often determine the maximum
achievable energy in a charged particle accelerator.
Let us investigate radiation losses in various different types
of accelerator device using the relativistic Larmor formula.
For a linear accelerator, the motion is one-dimensional. In this case,
it is easily demonstrated that
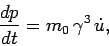 |
(1650) |
where use has been made of Eq. (1648), and
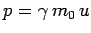 is
the particle momentum in the direction of acceleration
(the
is
the particle momentum in the direction of acceleration
(the  -direction, say). Here,
-direction, say). Here, 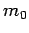 is the particle rest mass.
Thus, Eq. (1649) yields
is the particle rest mass.
Thus, Eq. (1649) yields
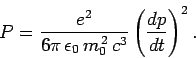 |
(1651) |
The rate of change of momentum is equal to the force exerted on the
particle in the  -direction, which, in turn, equals the change in the
energy,
-direction, which, in turn, equals the change in the
energy, 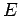 , of the particle per unit distance. Consequently,
, of the particle per unit distance. Consequently,
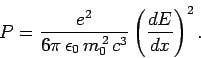 |
(1652) |
Thus, in a linear accelerator, the radiated power depends on the
external force acting on the particle, and not on the actual
energy or momentum of the particle.
It is obvious, from the above
formula, that light particles, such as electrons,
are going to radiate a lot more than heavier particles, such as protons.
The ratio of the power radiated to the power
supplied by the external sources is
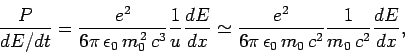 |
(1653) |
since  for a highly relativistic particle. It is
clear, from the above expression, that the radiation losses in an electron
linear accelerator are negligible unless the gain in energy is
of order
for a highly relativistic particle. It is
clear, from the above expression, that the radiation losses in an electron
linear accelerator are negligible unless the gain in energy is
of order
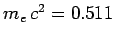 MeV in a distance of
MeV in a distance of
 meters. That is
meters. That is
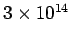 MeV/meter.
Typical energy gains are less that 10 MeV/meter. It follows, therefore,
that
radiation losses are completely negligible in linear accelerators, whether
for electrons, or for other heavier particles.
MeV/meter.
Typical energy gains are less that 10 MeV/meter. It follows, therefore,
that
radiation losses are completely negligible in linear accelerators, whether
for electrons, or for other heavier particles.
The situation is quite different in circular accelerator devices, such
as the synchrotron and the betatron. In such machines, the momentum 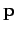 changes rapidly in direction as the particle rotates, but the change in energy
per revolution is small. Furthermore, the direction of acceleration is
always perpendicular to the direction of motion. It follows from
Eq. (1649) that
changes rapidly in direction as the particle rotates, but the change in energy
per revolution is small. Furthermore, the direction of acceleration is
always perpendicular to the direction of motion. It follows from
Eq. (1649) that
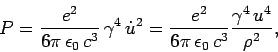 |
(1654) |
where 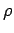 is the orbit radius. Here, use has been made of the standard
result
is the orbit radius. Here, use has been made of the standard
result
 for circular motion. The radiative
energy loss per revolution is given by
for circular motion. The radiative
energy loss per revolution is given by
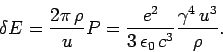 |
(1655) |
For highly relativistic ( ) electrons, this expression yields
) electrons, this expression yields
![\begin{displaymath}
\delta E ({\rm MeV}) = 8.85\times 10^{-2} \frac{[E({\rm GeV})]^4}{\rho
({\rm meters})}.
\end{displaymath}](img3333.png) |
(1656) |
In the first electron synchrotrons, 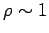 meter,
meter,
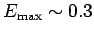 GeV. Hence,
GeV. Hence,
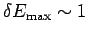 keV per revolution. This
was less than, but not negligible compared to, the energy gain of
a few keV per turn. For modern electron synchrotrons, the limitation
on the available radio-frequency power needed to overcome radiation
losses becomes a major consideration, as is clear from the
keV per revolution. This
was less than, but not negligible compared to, the energy gain of
a few keV per turn. For modern electron synchrotrons, the limitation
on the available radio-frequency power needed to overcome radiation
losses becomes a major consideration, as is clear from the 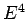 dependence of the radiated power per turn.
dependence of the radiated power per turn.



Next: Angular distribution of radiation
Up: Relativity and electromagnetism
Previous: The Larmor formula
Richard Fitzpatrick
2006-02-02
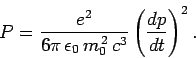
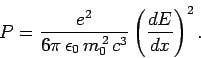
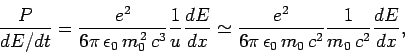
![]() changes rapidly in direction as the particle rotates, but the change in energy
per revolution is small. Furthermore, the direction of acceleration is
always perpendicular to the direction of motion. It follows from
Eq. (1649) that
changes rapidly in direction as the particle rotates, but the change in energy
per revolution is small. Furthermore, the direction of acceleration is
always perpendicular to the direction of motion. It follows from
Eq. (1649) that
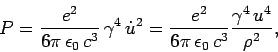
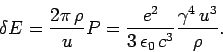
![\begin{displaymath}
\delta E ({\rm MeV}) = 8.85\times 10^{-2} \frac{[E({\rm GeV})]^4}{\rho
({\rm meters})}.
\end{displaymath}](img3333.png)