| (1354) | |||
| (1355) | |||
| (1356) |
| (1360) |
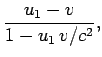 |
(1361) | ||
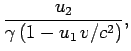 |
(1362) | ||
 |
(1363) |
Equations (1364)-(1366) can be regarded as giving the resultant,
![]() , of two velocities,
, of two velocities,
![]() and
and
![]() , and are therefore usually referred
to as the relativistic velocity addition formulae. The following
relation between the magnitudes
, and are therefore usually referred
to as the relativistic velocity addition formulae. The following
relation between the magnitudes
![]() and
and
![]() of the velocities
is easily demonstrated:
of the velocities
is easily demonstrated:
According to Eq. (1367), if ![]() then
then ![]() , no matter what
value
, no matter what
value ![]() takes: i.e., the velocity of light is invariant
between different inertial frames. Note that the Lorentz transform
only allows one such invariant velocity [i.e., the
velocity
takes: i.e., the velocity of light is invariant
between different inertial frames. Note that the Lorentz transform
only allows one such invariant velocity [i.e., the
velocity ![]() which appears in Eqs. (1346)-(1349)]. Einstein's relativity
principle tells us that any disturbance which propagates through a
vacuum must appear to propagate at the same velocity in all inertial
frames. It is now evident that all such disturbances must propagate
at the velocity
which appears in Eqs. (1346)-(1349)]. Einstein's relativity
principle tells us that any disturbance which propagates through a
vacuum must appear to propagate at the same velocity in all inertial
frames. It is now evident that all such disturbances must propagate
at the velocity ![]() . It follows immediately that
all electromagnetic waves must propagate through the vacuum with
this velocity, irrespective of their wavelength.
In other words, it is impossible for
there to be any dispersion of electromagnetic waves propagating through
a vacuum. Furthermore, gravity waves must also propagate with the
velocity
. It follows immediately that
all electromagnetic waves must propagate through the vacuum with
this velocity, irrespective of their wavelength.
In other words, it is impossible for
there to be any dispersion of electromagnetic waves propagating through
a vacuum. Furthermore, gravity waves must also propagate with the
velocity ![]() .
.
The Lorentz transformation implies that the velocities of propagation of all physical
effects are limited by ![]() in deterministic physics. Consider a general
process by which an event
in deterministic physics. Consider a general
process by which an event ![]() causes an event
causes an event ![]() at a
velocity
at a
velocity ![]() in some frame
in some frame ![]() . In other words, information
about the event
. In other words, information
about the event ![]() appears to propagate to the event
appears to propagate to the event ![]() with a
superluminal velocity. Let us choose coordinates such that these
two events occur on the
with a
superluminal velocity. Let us choose coordinates such that these
two events occur on the ![]() -axis with (finite) time and distance separations
-axis with (finite) time and distance separations
![]() and
and ![]() , respectively. The time separation in
some other inertial frame
, respectively. The time separation in
some other inertial frame ![]() is given by [see Eq. (1349)]
is given by [see Eq. (1349)]
| (1368) |