


Next: Rotation
Up: Vectors
Previous: The scalar product
We have discovered how to construct a scalar from the components of two
general vectors 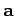 and
and 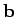 . Can we also construct a vector which is not
just a linear combination of
. Can we also construct a vector which is not
just a linear combination of 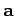 and
and 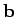 ? Consider the following definition:
? Consider the following definition:
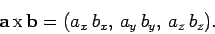 |
(28) |
Is
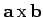 a proper vector? Suppose that
a proper vector? Suppose that
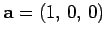 ,
,
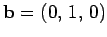 . Clearly,
. Clearly,
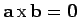 .
However, if we rotate the basis through
.
However, if we rotate the basis through 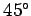 about the
about the 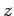 -axis then
-axis then
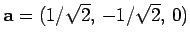 ,
,
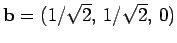 ,
and
,
and
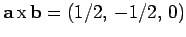 . Thus,
. Thus,
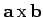 does
not transform like a vector, because its magnitude depends on the choice of axes.
So, above definition is a bad one.
does
not transform like a vector, because its magnitude depends on the choice of axes.
So, above definition is a bad one.
Consider, now, the cross product or vector product:
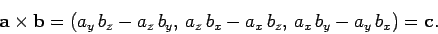 |
(29) |
Does this rather unlikely combination transform like a vector? Let us try
rotating the basis through 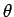 degrees about the
degrees about the 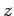 -axis using Eqs. (10)-(12).
In the new basis,
-axis using Eqs. (10)-(12).
In the new basis,
Thus, the 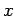 -component of
-component of
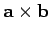 transforms correctly. It can
easily be shown that the other components transform correctly as well, and that
all components also transform correctly under rotation about the
transforms correctly. It can
easily be shown that the other components transform correctly as well, and that
all components also transform correctly under rotation about the 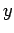 - and
- and 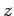 -axes.
Thus,
-axes.
Thus,
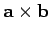 is a proper vector. Incidentally,
is a proper vector. Incidentally,
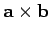 is the only simple combination of the components of two vectors which transforms
like a vector (which is non-coplanar with
is the only simple combination of the components of two vectors which transforms
like a vector (which is non-coplanar with 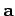 and
and 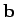 ).
The cross product is
anticommutative,
).
The cross product is
anticommutative,
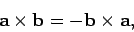 |
(31) |
distributive,
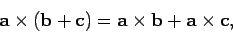 |
(32) |
but is not associative:
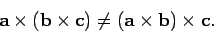 |
(33) |
The cross product transforms like a vector, which
means that it must have a well-defined direction and magnitude. We can show
that
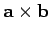 is perpendicular to both
is perpendicular to both 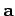 and
and 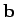 .
Consider
.
Consider
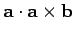 . If this is zero then the cross product
must be perpendicular to
. If this is zero then the cross product
must be perpendicular to 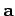 . Now
. Now
Therefore,
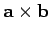 is perpendicular to
is perpendicular to 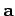 . Likewise, it can
be demonstrated that
. Likewise, it can
be demonstrated that
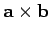 is perpendicular to
is perpendicular to 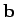 .
The vectors
.
The vectors 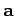 ,
, 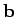 , and
, and
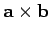 form a right-handed
set, like the unit vectors
form a right-handed
set, like the unit vectors 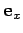 ,
, 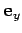 , and
, and 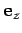 . In fact,
. In fact,
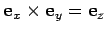 . This defines a unique direction for
. This defines a unique direction for
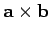 , which
is obtained from the right-hand rule (see Fig. 6).
, which
is obtained from the right-hand rule (see Fig. 6).
Figure 6:
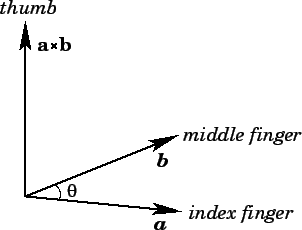 |
Let us now evaluate the magnitude of
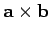 . We have
. We have
Thus,
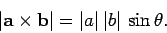 |
(36) |
Clearly,
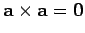 for any vector, since
for any vector, since  is always
zero in this case. Also, if
is always
zero in this case. Also, if
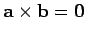 then either
then either
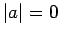 ,
, 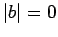 , or
, or 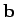 is parallel (or antiparallel) to
is parallel (or antiparallel) to 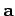 .
.
Figure 7:
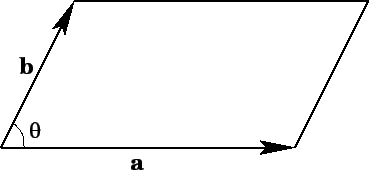 |
Consider the parallelogram defined by vectors 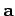 and
and 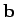 (see Fig. 7).
The scalar area is
(see Fig. 7).
The scalar area is
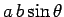 . The vector area has the magnitude of the
scalar area, and is normal to the plane of the parallelogram, which means that
it is perpendicular to both
. The vector area has the magnitude of the
scalar area, and is normal to the plane of the parallelogram, which means that
it is perpendicular to both 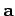 and
and 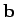 .
Clearly, the vector area
is given by
.
Clearly, the vector area
is given by
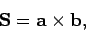 |
(37) |
with the sense obtained from the right-hand grip rule by rotating 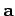 on to
on to
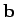 .
.
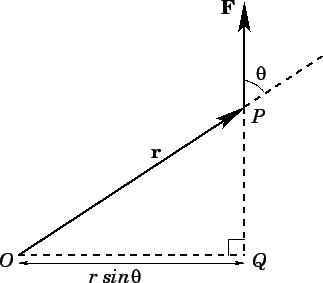
Suppose that a force 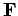 is applied at position
is applied at position 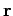 (see Fig. 8).
The moment, or torque, about the origin
(see Fig. 8).
The moment, or torque, about the origin 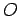 is the product of the magnitude of the force and
the length of the lever arm
is the product of the magnitude of the force and
the length of the lever arm 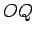 . Thus, the magnitude of the moment is
. Thus, the magnitude of the moment is
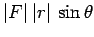 . The direction of the moment is conventionally the direction of
the axis through
. The direction of the moment is conventionally the direction of
the axis through 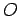 about which the force tries to rotate objects, in the sense
determined by the right-hand grip rule. It follows that the vector moment is
given by
about which the force tries to rotate objects, in the sense
determined by the right-hand grip rule. It follows that the vector moment is
given by
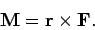 |
(38) |
Figure 8:
 |



Next: Rotation
Up: Vectors
Previous: The scalar product
Richard Fitzpatrick
2006-02-02
![]() is perpendicular to both
is perpendicular to both ![]() and
and ![]() .
Consider
.
Consider
![]() . If this is zero then the cross product
must be perpendicular to
. If this is zero then the cross product
must be perpendicular to ![]() . Now
. Now
![]() . We have
. We have
![]() is applied at position
is applied at position ![]() (see Fig. 8).
The moment, or torque, about the origin
(see Fig. 8).
The moment, or torque, about the origin ![]() is the product of the magnitude of the force and
the length of the lever arm
is the product of the magnitude of the force and
the length of the lever arm ![]() . Thus, the magnitude of the moment is
. Thus, the magnitude of the moment is
![]() . The direction of the moment is conventionally the direction of
the axis through
. The direction of the moment is conventionally the direction of
the axis through ![]() about which the force tries to rotate objects, in the sense
determined by the right-hand grip rule. It follows that the vector moment is
given by
about which the force tries to rotate objects, in the sense
determined by the right-hand grip rule. It follows that the vector moment is
given by