Next: Stability of Lagrange points Up: Three-body problem Previous: Lagrange points
 |
(9.61) |
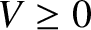 .
It follows, from Equation (9.35), that if the mass
.
It follows, from Equation (9.35), that if the mass  has the Jacobi
integral
has the Jacobi
integral  and lies on the surface specified in Equation (9.60),
then it must have zero velocity. Hence, such a surface is termed a
zero-velocity surface. The zero-velocity surfaces are important
because they form the boundary of regions from which
the mass
and lies on the surface specified in Equation (9.60),
then it must have zero velocity. Hence, such a surface is termed a
zero-velocity surface. The zero-velocity surfaces are important
because they form the boundary of regions from which
the mass  is dynamically excluded; that is, regions where
is dynamically excluded; that is, regions where 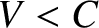 .
Generally speaking, the regions from which
.
Generally speaking, the regions from which  is excluded grow in area as
is excluded grow in area as
 increases, and vice versa.
increases, and vice versa.
Let 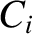 be the value of
be the value of 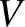 at the
at the 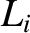 Lagrange point, for
Lagrange point, for  . When
. When
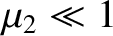 ,
it is easily demonstrated that
,
it is easily demonstrated that
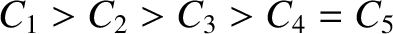 .
.
![\includegraphics[height=3.25in]{Chapter08/fig8_07.eps}](img2239.png)
|
![\includegraphics[height=3.25in]{Chapter08/fig8_08.eps}](img2240.png)
|
![\includegraphics[height=3.25in]{Chapter08/fig8_09.eps}](img2241.png)
|
![\includegraphics[height=3.25in]{Chapter08/fig8_10.eps}](img2242.png)
|
![\includegraphics[height=3.25in]{Chapter08/fig8_11.eps}](img2243.png)
|
Figures 9.7 through 9.11 show the intersection of the zero-velocity
surface  with the
with the  -
- plane for various different values of
plane for various different values of  , and
illustrate how the region from which
, and
illustrate how the region from which  is dynamically excluded—which we shall term the excluded region—evolves as the value of
is dynamically excluded—which we shall term the excluded region—evolves as the value of
 is varied. Of course, any point not in the excluded region is in the so-called allowed region.
For
is varied. Of course, any point not in the excluded region is in the so-called allowed region.
For  , the allowed region consists of two
separate oval regions centered on
, the allowed region consists of two
separate oval regions centered on 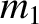 and
and 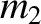 , respectively, plus an
outer region that lies beyond a
large circle centered on the origin. All three allowed regions are separated
from one another by an excluded region. See Figure 9.7. When
, respectively, plus an
outer region that lies beyond a
large circle centered on the origin. All three allowed regions are separated
from one another by an excluded region. See Figure 9.7. When 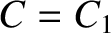 ,
the two inner allowed regions merge at the
,
the two inner allowed regions merge at the 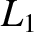 point. See Figure 9.8.
When
point. See Figure 9.8.
When 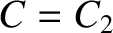 , the inner and outer allowed regions merge at the
, the inner and outer allowed regions merge at the 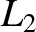 point, forming a horseshoe-like excluded region. See Figure 9.9.
When
point, forming a horseshoe-like excluded region. See Figure 9.9.
When 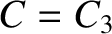 , the excluded region splits in two at the
, the excluded region splits in two at the 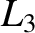 point. See Figure 9.10.
For
point. See Figure 9.10.
For
 , the two excluded regions are localized about the
, the two excluded regions are localized about the
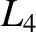 and
and
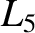 points. See Figure 9.11. Finally, for
points. See Figure 9.11. Finally, for 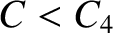 , there is no excluded
region.
, there is no excluded
region.
Figure 9.12 shows the zero-velocity surfaces and Lagrange points
calculated for the case
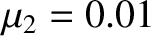 . It can be seen that, at very small values of
. It can be seen that, at very small values of
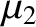 , the
, the 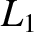 and
and 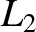 Lagrange points are almost equidistant from mass
Lagrange points are almost equidistant from mass 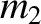 .
Furthermore, mass
.
Furthermore, mass 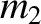 , and the
, and the 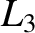 ,
, 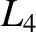 , and
, and 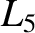 Lagrange points all lie approximately
on a unit circle,
centered on mass
Lagrange points all lie approximately
on a unit circle,
centered on mass 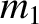 . It follows that, when
. It follows that, when 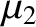 is small, the Lagrange points
is small, the Lagrange points 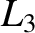 ,
, 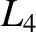 and
and 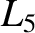 all
share the orbit of mass
all
share the orbit of mass 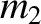 about
about 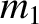 (in the inertial frame) with
(in the inertial frame) with 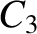 being directly opposite
being directly opposite 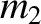 ,
,
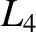 (by convention)
(by convention) 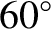 ahead of
ahead of 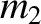 , and
, and 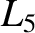
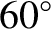 behind.
behind.