Next: Tisserand criterion Up: Three-body problem Previous: Circular restricted three-body problem
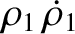 |
 |
(9.12) |
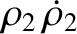 |
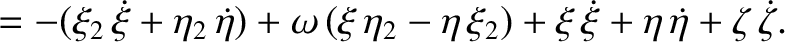 |
(9.13) |
 |
(9.14) |
 —which is usually referred to as the Jacobi integral—is a
constant of the motion.
—which is usually referred to as the Jacobi integral—is a
constant of the motion.
We can rearrange Equation (9.10) to give
where is the energy (per unit mass) of mass
is the energy (per unit mass) of mass  ,
,
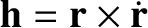 the angular momentum
(per unit mass) of mass
the angular momentum
(per unit mass) of mass  , and
, and
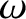
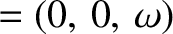 the orbital angular velocity of the other two masses.
Note, however, that
the orbital angular velocity of the other two masses.
Note, however, that 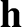 is not a constant of the motion. Hence,
is not a constant of the motion. Hence,  is not
a constant of the motion either. In fact, the Jacobi integral is the only constant of the
motion in the circular restricted three-body problem. Incidentally, the energy
of mass
is not
a constant of the motion either. In fact, the Jacobi integral is the only constant of the
motion in the circular restricted three-body problem. Incidentally, the energy
of mass  is not a conserved quantity because the other two masses in the system
are moving.
is not a conserved quantity because the other two masses in the system
are moving.