Next: Jacobi integral Up: Three-body problem Previous: Introduction
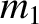 ,
, 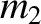 , and
, and  .
Suppose, however, that the third mass,
.
Suppose, however, that the third mass,  , is so much smaller than the other two that it has a negligible
effect on their motion. Suppose, further, that the first two masses,
, is so much smaller than the other two that it has a negligible
effect on their motion. Suppose, further, that the first two masses, 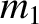 and
and 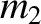 , execute circular
orbits about their common center of mass. In the following, we shall examine this simplified problem, which is usually
referred to as the circular restricted
three-body problem. The problem under investigation has obvious applications to the solar system. For instance, the first two masses might represent
the Sun and a planet (recall that a given planet and the Sun do indeed execute almost circular orbits about their common center of mass),
whereas the third mass might represent an asteroid or a comet (asteroids and comets do indeed have much smaller masses than the Sun or
any of the planets).
, execute circular
orbits about their common center of mass. In the following, we shall examine this simplified problem, which is usually
referred to as the circular restricted
three-body problem. The problem under investigation has obvious applications to the solar system. For instance, the first two masses might represent
the Sun and a planet (recall that a given planet and the Sun do indeed execute almost circular orbits about their common center of mass),
whereas the third mass might represent an asteroid or a comet (asteroids and comets do indeed have much smaller masses than the Sun or
any of the planets).
Let us define a Cartesian coordinate system
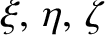 in an inertial reference frame whose
origin coincides with the center of mass,
in an inertial reference frame whose
origin coincides with the center of mass,  , of the two orbiting masses,
, of the two orbiting masses, 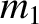 and
and 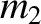 . Furthermore, let the orbital plane of these masses
coincide with the
. Furthermore, let the orbital plane of these masses
coincide with the 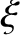 -
- plane, and let them both lie on the
plane, and let them both lie on the 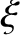 -axis at time
-axis at time 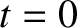 . See Figure 9.1.
Suppose that
. See Figure 9.1.
Suppose that  is the constant distance between the two orbiting masses,
is the constant distance between the two orbiting masses,  the constant distance
between mass
the constant distance
between mass 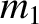 and the origin, and
and the origin, and 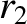 the constant distance between mass
the constant distance between mass 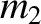 and the origin. Moreover,
let
and the origin. Moreover,
let 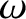 be the constant orbital angular velocity. It follows, from Section 4.16,
that
be the constant orbital angular velocity. It follows, from Section 4.16,
that
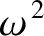 |
 |
(9.1) |
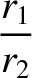 |
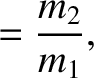 |
(9.2) |
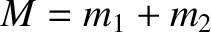 .
.
It is convenient to choose our unit of length such that 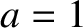 , and our unit of
mass such that
, and our unit of
mass such that 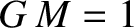 . It follows, from Equation (9.1), that
. It follows, from Equation (9.1), that 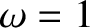 . However, we shall continue to
retain
. However, we shall continue to
retain 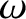 in our equations, for the sake of clarity. Let
in our equations, for the sake of clarity. Let
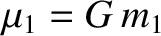 and
and
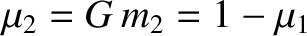 . It is easily demonstrated
that
. It is easily demonstrated
that
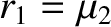 and
and
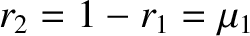 . Hence, the two orbiting masses,
. Hence, the two orbiting masses, 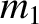 and
and 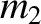 , have position
vectors
, have position
vectors
 . The
Cartesian components of the equation of motion of this mass are thus
where
. The
Cartesian components of the equation of motion of this mass are thus
where