Generalized momenta
Consider the motion of a single particle moving in one dimension. The
kinetic energy is
 |
(7.33) |
where  is the mass of the particle and
is the mass of the particle and  its displacement.
The particle's linear momentum is
its displacement.
The particle's linear momentum is
 . However,
this can also be written
. However,
this can also be written
 |
(7.34) |
because
 and the potential energy
and the potential energy 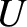 is independent of
is independent of
 .
.
Consider a dynamical system described by 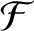 generalized coordinates
generalized coordinates
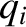 , for
, for
 . By analogy with the preceding expression, we can
define generalized momenta of the form
. By analogy with the preceding expression, we can
define generalized momenta of the form
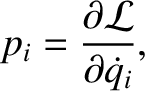 |
(7.35) |
for
 . Here,
. Here,  is sometimes called the momentum conjugate to the coordinate
is sometimes called the momentum conjugate to the coordinate 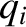 . Hence, Lagrange's equation (7.22) can be written
. Hence, Lagrange's equation (7.22) can be written
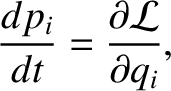 |
(7.36) |
for
 . Note that a generalized momentum does not necessarily have
the dimensions of linear momentum.
. Note that a generalized momentum does not necessarily have
the dimensions of linear momentum.
Suppose that the Lagrangian  does not depend explicitly on some coordinate
does not depend explicitly on some coordinate
 . It follows from Equation (7.36) that
. It follows from Equation (7.36) that
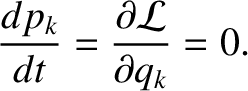 |
(7.37) |
Hence,
 |
(7.38) |
The coordinate  is said to be ignorable in this case.
Thus, we conclude that the generalized momentum associated with
an ignorable coordinate is a constant of the motion.
is said to be ignorable in this case.
Thus, we conclude that the generalized momentum associated with
an ignorable coordinate is a constant of the motion.
For example, the Lagrangian [Equation (7.24)] for a
particle moving in a central potential is independent of the angular
coordinate  . Thus,
. Thus,  is an ignorable coordinate,
and
is an ignorable coordinate,
and
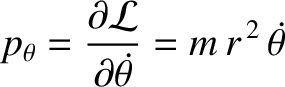 |
(7.39) |
is a constant of the motion. Of course,  is the angular momentum
about the origin; this is conserved because a central force exerts no torque
about the origin.
is the angular momentum
about the origin; this is conserved because a central force exerts no torque
about the origin.

 is the mass of the particle and
is the mass of the particle and  its displacement.
The particle's linear momentum is
its displacement.
The particle's linear momentum is
 . However,
this can also be written
. However,
this can also be written

 and the potential energy
and the potential energy 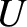 is independent of
is independent of
 .
.
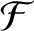 generalized coordinates
generalized coordinates
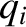 , for
, for
 . By analogy with the preceding expression, we can
define generalized momenta of the form
. By analogy with the preceding expression, we can
define generalized momenta of the form
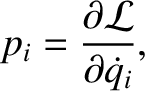
 . Here,
. Here,  is sometimes called the momentum conjugate to the coordinate
is sometimes called the momentum conjugate to the coordinate 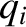 . Hence, Lagrange's equation (7.22) can be written
for
. Hence, Lagrange's equation (7.22) can be written
for
 . Note that a generalized momentum does not necessarily have
the dimensions of linear momentum.
. Note that a generalized momentum does not necessarily have
the dimensions of linear momentum.
 does not depend explicitly on some coordinate
does not depend explicitly on some coordinate
 . It follows from Equation (7.36) that
. It follows from Equation (7.36) that
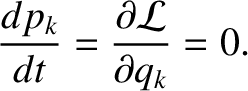

 is said to be ignorable in this case.
Thus, we conclude that the generalized momentum associated with
an ignorable coordinate is a constant of the motion.
is said to be ignorable in this case.
Thus, we conclude that the generalized momentum associated with
an ignorable coordinate is a constant of the motion.
 . Thus,
. Thus,  is an ignorable coordinate,
and
is an ignorable coordinate,
and
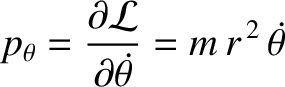
 is the angular momentum
about the origin; this is conserved because a central force exerts no torque
about the origin.
is the angular momentum
about the origin; this is conserved because a central force exerts no torque
about the origin.