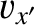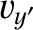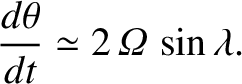Coriolis force
We have now accounted for the first fictitious force,


 , appearing in Equation (6.9).
Let us now investigate the second, which takes the form
, appearing in Equation (6.9).
Let us now investigate the second, which takes the form
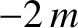

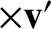 , and is called the Coriolis force.
Obviously, this force only affects objects that are moving in the rotating
reference frame.
, and is called the Coriolis force.
Obviously, this force only affects objects that are moving in the rotating
reference frame.
Consider a particle of mass  free-falling under gravity in our rotating reference frame. As before, we define Cartesian axes in the rotating frame such that the
free-falling under gravity in our rotating reference frame. As before, we define Cartesian axes in the rotating frame such that the 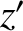 -axis
points vertically upward and the
-axis
points vertically upward and the 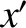 - and
- and 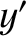 -axes are horizontal, with
the
-axes are horizontal, with
the 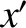 -axis pointing directly northward and the
-axis pointing directly northward and the 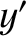 -axis pointing directly
westward. It follows, from Equation (6.9), that the Cartesian equations of motion of the particle
in the rotating reference frame take the form
-axis pointing directly
westward. It follows, from Equation (6.9), that the Cartesian equations of motion of the particle
in the rotating reference frame take the form
Here, 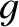 is the local acceleration due to gravity. In the
preceding three equations, we have neglected the centrifugal acceleration, for the sake
of simplicity. This is reasonable, because the only effect of the centrifugal
acceleration is to slightly modify the magnitude and direction of the
local gravitational acceleration. We have also neglected air resistance,
which is less reasonable.
is the local acceleration due to gravity. In the
preceding three equations, we have neglected the centrifugal acceleration, for the sake
of simplicity. This is reasonable, because the only effect of the centrifugal
acceleration is to slightly modify the magnitude and direction of the
local gravitational acceleration. We have also neglected air resistance,
which is less reasonable.
Consider a particle that is dropped (at 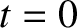 ) from rest a height
) from rest a height 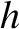 above the Earth's
surface. The following solution method exploits the fact that the
Coriolis force is much smaller in magnitude that the force of gravity. Hence,
above the Earth's
surface. The following solution method exploits the fact that the
Coriolis force is much smaller in magnitude that the force of gravity. Hence,
 can be treated as a small parameter.
To lowest order (i.e., neglecting
can be treated as a small parameter.
To lowest order (i.e., neglecting
 ), the
particle's vertical motion satisfies
), the
particle's vertical motion satisfies
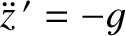 , which can be solved,
subject to the initial conditions, to give
, which can be solved,
subject to the initial conditions, to give
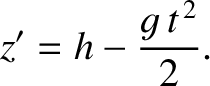 |
(6.22) |
Substituting this expression into Equations (6.19) and (6.20),
neglecting terms involving
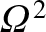 , and solving subject to the
initial conditions, we obtain
, and solving subject to the
initial conditions, we obtain
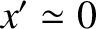 and
and
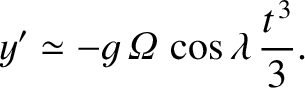 |
(6.23) |
In other words, the particle is deflected eastward (i.e., in the negative
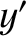 -direction). The particle hits the ground when
-direction). The particle hits the ground when
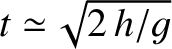 . Hence, the net eastward deflection of the particle as it strikes the ground is
. Hence, the net eastward deflection of the particle as it strikes the ground is
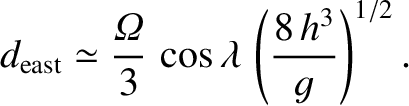 |
(6.24) |
This deflection is in the same direction as the Earth's rotation (i.e., west to east)
and is greatest at the equator, and zero at the poles.
A particle dropped from a height of 100 m at the equator is deflected by about
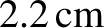 .
.
Consider a particle launched horizontally with some fairly large velocity
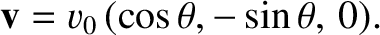 |
(6.25) |
Here,  is the compass
bearing of the velocity vector (so north is
is the compass
bearing of the velocity vector (so north is 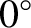 , east is
, east is 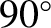 , etc.). Neglecting any vertical motion, Equations (6.19) and (6.20) yield
which can be integrated to give
To lowest order in
, etc.). Neglecting any vertical motion, Equations (6.19) and (6.20) yield
which can be integrated to give
To lowest order in
 , the preceding equations are equivalent to
It follows that the Coriolis force causes the compass
bearing of the particle's velocity vector to rotate steadily as time progresses. The rotation rate is
, the preceding equations are equivalent to
It follows that the Coriolis force causes the compass
bearing of the particle's velocity vector to rotate steadily as time progresses. The rotation rate is
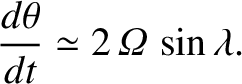 |
(6.32) |
Hence, the rotation is clockwise (if we look from above) in the
northern hemisphere, and counterclockwise in the
southern hemisphere. The rotation rate is zero at the equator and
greatest at the poles.
The Coriolis force has a significant effect on terrestrial weather patterns.
Near equatorial regions, the Sun's intense heating of the Earth's surface causes hot
air to rise. In the northern hemisphere, this causes cooler air to
move in a southerly direction toward the equator. The Coriolis
force deflects this moving air in a clockwise sense (if we look from above),
resulting in the trade winds, which blow toward the southwest.
In the southern hemisphere, the cooler air moves northward and
is deflected by the Coriolis force in a counterclockwise sense, resulting
in trade winds that blow toward the northwest.
Furthermore, as air flows from high- to low-pressure regions,
the Coriolis force deflects the air in a clockwise/counterclockwise manner in the northern/southern
hemisphere, producing cyclonic rotation. See Figure 6.3.
It follows that cyclonic rotation is counterclockwise (seen from above) in the northern hemisphere,
and clockwise in the southern hemisphere. Thus, this
is the direction of rotation of tropical storms (e.g., hurricanes,
typhoons) in each hemisphere.
Figure 6.3:
Cyclone in Earth's northern hemisphere.
|
|
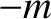

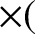

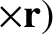 , appearing in Equation (6.9).
Let us now investigate the second, which takes the form
, appearing in Equation (6.9).
Let us now investigate the second, which takes the form
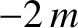

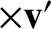 , and is called the Coriolis force.
Obviously, this force only affects objects that are moving in the rotating
reference frame.
, and is called the Coriolis force.
Obviously, this force only affects objects that are moving in the rotating
reference frame.
 free-falling under gravity in our rotating reference frame. As before, we define Cartesian axes in the rotating frame such that the
free-falling under gravity in our rotating reference frame. As before, we define Cartesian axes in the rotating frame such that the 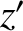 -axis
points vertically upward and the
-axis
points vertically upward and the 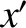 - and
- and 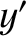 -axes are horizontal, with
the
-axes are horizontal, with
the 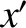 -axis pointing directly northward and the
-axis pointing directly northward and the 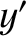 -axis pointing directly
westward. It follows, from Equation (6.9), that the Cartesian equations of motion of the particle
in the rotating reference frame take the form
-axis pointing directly
westward. It follows, from Equation (6.9), that the Cartesian equations of motion of the particle
in the rotating reference frame take the form
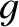 is the local acceleration due to gravity. In the
preceding three equations, we have neglected the centrifugal acceleration, for the sake
of simplicity. This is reasonable, because the only effect of the centrifugal
acceleration is to slightly modify the magnitude and direction of the
local gravitational acceleration. We have also neglected air resistance,
which is less reasonable.
is the local acceleration due to gravity. In the
preceding three equations, we have neglected the centrifugal acceleration, for the sake
of simplicity. This is reasonable, because the only effect of the centrifugal
acceleration is to slightly modify the magnitude and direction of the
local gravitational acceleration. We have also neglected air resistance,
which is less reasonable.
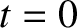 ) from rest a height
) from rest a height 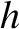 above the Earth's
surface. The following solution method exploits the fact that the
Coriolis force is much smaller in magnitude that the force of gravity. Hence,
above the Earth's
surface. The following solution method exploits the fact that the
Coriolis force is much smaller in magnitude that the force of gravity. Hence,
 can be treated as a small parameter.
To lowest order (i.e., neglecting
can be treated as a small parameter.
To lowest order (i.e., neglecting
 ), the
particle's vertical motion satisfies
), the
particle's vertical motion satisfies
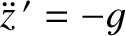 , which can be solved,
subject to the initial conditions, to give
, which can be solved,
subject to the initial conditions, to give
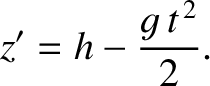
 , and solving subject to the
initial conditions, we obtain
, and solving subject to the
initial conditions, we obtain
 and
and
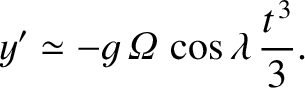
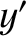 -direction). The particle hits the ground when
-direction). The particle hits the ground when
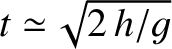 . Hence, the net eastward deflection of the particle as it strikes the ground is
. Hence, the net eastward deflection of the particle as it strikes the ground is
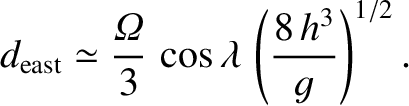
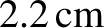 .
.
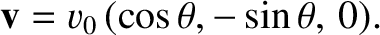
 is the compass
bearing of the velocity vector (so north is
is the compass
bearing of the velocity vector (so north is 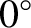 , east is
, east is 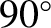 , etc.). Neglecting any vertical motion, Equations (6.19) and (6.20) yield
, etc.). Neglecting any vertical motion, Equations (6.19) and (6.20) yield
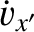
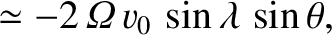
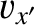
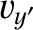
 , the preceding equations are equivalent to
, the preceding equations are equivalent to