Motion in nearly circular orbit
In principle, a circular orbit is a possible orbit for any attractive central force.
However, not all such forces result in stable circular orbits.
Let us now consider the stability of circular orbits in a general central force field. Equation (4.25) generalizes to
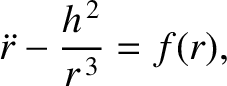 |
(5.7) |
where
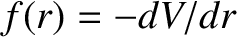 is the radial force per unit mass. For a circular orbit,
is the radial force per unit mass. For a circular orbit,
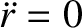 , and the preceding equation reduces to
, and the preceding equation reduces to
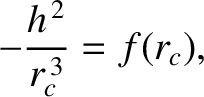 |
(5.8) |
where 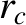 is the radius of the orbit.
is the radius of the orbit.
Let us now consider small departures from circularity. Suppose that
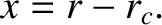 |
(5.9) |
Equation (5.7) can be written
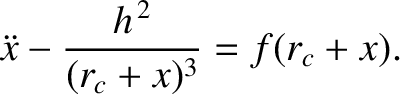 |
(5.10) |
Expanding the two terms involving 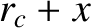 as power series in
as power series in 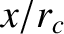 ,
and keeping all terms up to first order, we obtain
,
and keeping all terms up to first order, we obtain
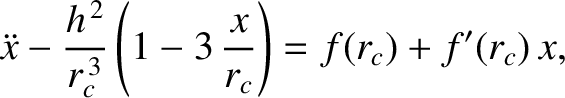 |
(5.11) |
where 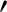 denotes a derivative. Making use of Equation (5.8),
the preceding equation reduces to
denotes a derivative. Making use of Equation (5.8),
the preceding equation reduces to
![$\displaystyle \ddot{x} + \left[-\frac{3\,f(r_c)}{r_c} - f'(r_c)\right] x = 0.$](img966.png) |
(5.12) |
If the term in square brackets is positive then we obtain a simple harmonic
equation, which we already know has bounded solutions (see Section 2.8); in other words, the orbit is stable to small perturbations. On the other hand,
if the term is square brackets is negative then we obtain an equation
whose solutions grow exponentially in time (see Section 2.8); in other words, the orbit
is unstable to small perturbations. Thus, the stability criterion for a circular
orbit of radius 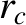 in a central force field characterized by a radial force
(per unit mass) function
in a central force field characterized by a radial force
(per unit mass) function 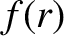 is
is
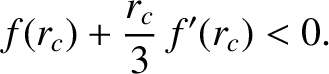 |
(5.13) |
For example, consider an attractive power-law force function of the form
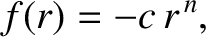 |
(5.14) |
where 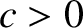 . Substituting into the preceding stability criterion, we obtain
. Substituting into the preceding stability criterion, we obtain
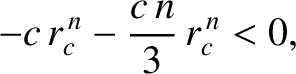 |
(5.15) |
or
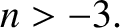 |
(5.16) |
We conclude that circular orbits in attractive central force fields that decay
faster than 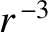 are unstable. The case
are unstable. The case 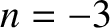 is special, because the first-order terms in the expansion of Equation (5.10) cancel out exactly, and it
is necessary to retain the second-order terms. Doing this, we can easily demonstrate that circular orbits are also unstable for
inverse-cube (
is special, because the first-order terms in the expansion of Equation (5.10) cancel out exactly, and it
is necessary to retain the second-order terms. Doing this, we can easily demonstrate that circular orbits are also unstable for
inverse-cube (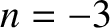 ) forces. (See Section 5.6, Exercise 9.)
) forces. (See Section 5.6, Exercise 9.)
An apsis (plural, apsides) is a point on an orbit at which the radial distance,  , assumes either a
maximum or a minimum value. Thus, the perihelion and aphelion points
are the apsides of planetary orbits. The angle through which the radius vector
rotates in going between two consecutive apsides is called the apsidal
angle. Hence, the apsidal angle for elliptical orbits in an inverse-square
force field is
, assumes either a
maximum or a minimum value. Thus, the perihelion and aphelion points
are the apsides of planetary orbits. The angle through which the radius vector
rotates in going between two consecutive apsides is called the apsidal
angle. Hence, the apsidal angle for elliptical orbits in an inverse-square
force field is 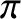 .
.
For the case of stable, nearly circular orbits, we have seen that  oscillates sinusoidally
about its mean value,
oscillates sinusoidally
about its mean value, 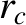 . Indeed, it is clear from Equation (5.12) that
the period of the oscillation is
. Indeed, it is clear from Equation (5.12) that
the period of the oscillation is
![$\displaystyle T = \frac{2\pi}{\left[-3\,f(r_c)/r_c - f'(r_c)\right]^{1/2}}.$](img975.png) |
(5.17) |
The apsidal angle is the amount by which  increases in going
between a maximum and a minimum of
increases in going
between a maximum and a minimum of  . The time taken
to achieve this is clearly
. The time taken
to achieve this is clearly 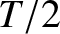 . Now,
. Now,
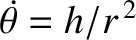 , where
, where 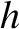 is a constant of the motion, and
is a constant of the motion, and  is almost constant. Thus,
is almost constant. Thus,
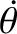 is approximately constant. In fact,
is approximately constant. In fact,
![$\displaystyle \skew{5}\dot{\theta} \simeq \frac{h}{r_c^{\,2}} = \left[-\frac{f(r_c)}{r_c}\right]^{1/2},$](img979.png) |
(5.18) |
where use has been made of Equation (5.8). Thus, the apsidal angle,
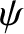 ,
is given by
,
is given by
![$\displaystyle \psi = \frac{T}{2}\, \skew{5}\dot{\theta} = \pi \left[3+r_c\,\frac{f'(r_c)}{f(r_c)}\right]^{-1/2}$](img981.png) |
(5.19) |
For the case of attractive power-law central forces of the form
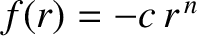 , where
, where
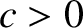 , the apsidal angle becomes
, the apsidal angle becomes
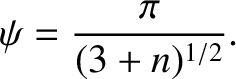 |
(5.20) |
It should be clear that if an orbit is going to close on itself then the apsidal angle needs to be a rational fraction of 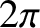 . There are, in fact,
only two small-integer values of the power-law index,
. There are, in fact,
only two small-integer values of the power-law index, 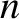 , for which this
is the case. As we have already seen, for an inverse-square force law (i.e.,
, for which this
is the case. As we have already seen, for an inverse-square force law (i.e., 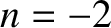 ), the
apsidal angle is
), the
apsidal angle is 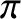 . Moreover, for a linear force law (i.e.,
. Moreover, for a linear force law (i.e., 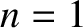 ),
the apsidal angle is
),
the apsidal angle is 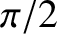 . However, for quadratic (i.e.,
. However, for quadratic (i.e., 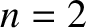 ) or cubic (i.e.,
) or cubic (i.e., 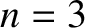 ) force laws, the apsidal angle is an irrational
fraction of
) force laws, the apsidal angle is an irrational
fraction of 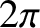 , which means that non-circular orbits in such force fields
never close on themselves.
, which means that non-circular orbits in such force fields
never close on themselves.
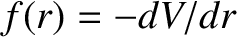 is the radial force per unit mass. For a circular orbit,
is the radial force per unit mass. For a circular orbit,
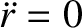 , and the preceding equation reduces to
where
, and the preceding equation reduces to
where 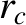 is the radius of the orbit.
is the radius of the orbit.
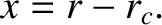
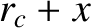 as power series in
as power series in 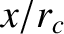 ,
and keeping all terms up to first order, we obtain
,
and keeping all terms up to first order, we obtain
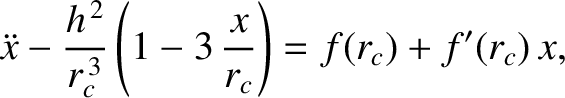
 denotes a derivative. Making use of Equation (5.8),
the preceding equation reduces to
If the term in square brackets is positive then we obtain a simple harmonic
equation, which we already know has bounded solutions (see Section 2.8); in other words, the orbit is stable to small perturbations. On the other hand,
if the term is square brackets is negative then we obtain an equation
whose solutions grow exponentially in time (see Section 2.8); in other words, the orbit
is unstable to small perturbations. Thus, the stability criterion for a circular
orbit of radius
denotes a derivative. Making use of Equation (5.8),
the preceding equation reduces to
If the term in square brackets is positive then we obtain a simple harmonic
equation, which we already know has bounded solutions (see Section 2.8); in other words, the orbit is stable to small perturbations. On the other hand,
if the term is square brackets is negative then we obtain an equation
whose solutions grow exponentially in time (see Section 2.8); in other words, the orbit
is unstable to small perturbations. Thus, the stability criterion for a circular
orbit of radius 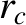 in a central force field characterized by a radial force
(per unit mass) function
in a central force field characterized by a radial force
(per unit mass) function 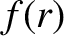 is
is
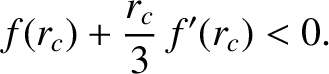
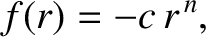
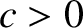 . Substituting into the preceding stability criterion, we obtain
. Substituting into the preceding stability criterion, we obtain
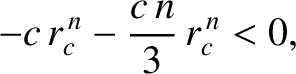
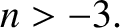
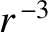 are unstable. The case
are unstable. The case 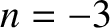 is special, because the first-order terms in the expansion of Equation (5.10) cancel out exactly, and it
is necessary to retain the second-order terms. Doing this, we can easily demonstrate that circular orbits are also unstable for
inverse-cube (
is special, because the first-order terms in the expansion of Equation (5.10) cancel out exactly, and it
is necessary to retain the second-order terms. Doing this, we can easily demonstrate that circular orbits are also unstable for
inverse-cube (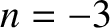 ) forces. (See Section 5.6, Exercise 9.)
) forces. (See Section 5.6, Exercise 9.)
 , assumes either a
maximum or a minimum value. Thus, the perihelion and aphelion points
are the apsides of planetary orbits. The angle through which the radius vector
rotates in going between two consecutive apsides is called the apsidal
angle. Hence, the apsidal angle for elliptical orbits in an inverse-square
force field is
, assumes either a
maximum or a minimum value. Thus, the perihelion and aphelion points
are the apsides of planetary orbits. The angle through which the radius vector
rotates in going between two consecutive apsides is called the apsidal
angle. Hence, the apsidal angle for elliptical orbits in an inverse-square
force field is 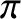 .
.
 oscillates sinusoidally
about its mean value,
oscillates sinusoidally
about its mean value, 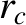 . Indeed, it is clear from Equation (5.12) that
the period of the oscillation is
. Indeed, it is clear from Equation (5.12) that
the period of the oscillation is
![$\displaystyle T = \frac{2\pi}{\left[-3\,f(r_c)/r_c - f'(r_c)\right]^{1/2}}.$](img975.png)
 increases in going
between a maximum and a minimum of
increases in going
between a maximum and a minimum of  . The time taken
to achieve this is clearly
. The time taken
to achieve this is clearly 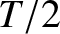 . Now,
. Now,
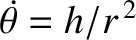 , where
, where 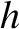 is a constant of the motion, and
is a constant of the motion, and  is almost constant. Thus,
is almost constant. Thus,
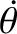 is approximately constant. In fact,
is approximately constant. In fact,
![$\displaystyle \skew{5}\dot{\theta} \simeq \frac{h}{r_c^{\,2}} = \left[-\frac{f(r_c)}{r_c}\right]^{1/2},$](img979.png)
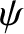 ,
is given by
,
is given by
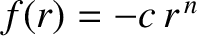 , where
, where
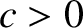 , the apsidal angle becomes
, the apsidal angle becomes
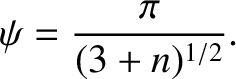
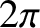 . There are, in fact,
only two small-integer values of the power-law index,
. There are, in fact,
only two small-integer values of the power-law index, 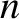 , for which this
is the case. As we have already seen, for an inverse-square force law (i.e.,
, for which this
is the case. As we have already seen, for an inverse-square force law (i.e., 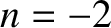 ), the
apsidal angle is
), the
apsidal angle is 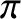 . Moreover, for a linear force law (i.e.,
. Moreover, for a linear force law (i.e., 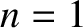 ),
the apsidal angle is
),
the apsidal angle is 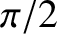 . However, for quadratic (i.e.,
. However, for quadratic (i.e., 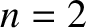 ) or cubic (i.e.,
) or cubic (i.e., 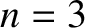 ) force laws, the apsidal angle is an irrational
fraction of
) force laws, the apsidal angle is an irrational
fraction of 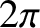 , which means that non-circular orbits in such force fields
never close on themselves.
, which means that non-circular orbits in such force fields
never close on themselves.