Next: Motion in nearly circular Up: Orbits in central force Previous: Introduction
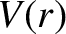 . Because the
force field
is central, it still remains true that
is a constant of the motion. (See Section 4.5.) As is easily demonstrated, Equation (4.28)
generalizes to
where
. Because the
force field
is central, it still remains true that
is a constant of the motion. (See Section 4.5.) As is easily demonstrated, Equation (4.28)
generalizes to
where
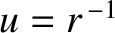 .
.
Suppose, for instance, that we wish to find the potential 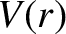 that causes
an object to execute the spiral orbit
that causes
an object to execute the spiral orbit
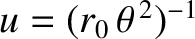 into Equation (5.2) yields
into Equation (5.2) yields
 |
(5.4) |
 |
(5.5) |
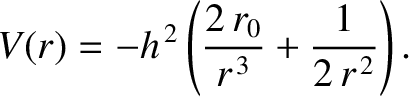 |
(5.6) |