Simple application of Darwin-Radau theory
As a simple application of the preceding analysis, let us assume that the density distribution inside the rotating body is such that
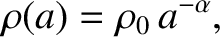 |
(D.54) |
for
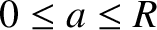 , where
, where
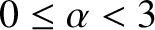 . Of course,
. Of course, 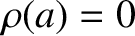 for
for 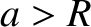 . According to Equations (D.26) and (D.42),
. According to Equations (D.26) and (D.42),
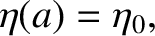 |
(D.55) |
where
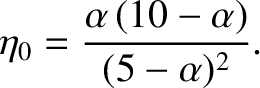 |
(D.56) |
Thus, Equation (D.33) yields
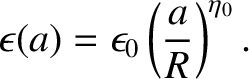 |
(D.57) |
Finally, it follows from Equations (D.48), (D.49), and (D.51) that
respectively.
For the case of the Earth (Yoder 1995),
These values are consistent with formula (D.59) provided
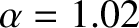 , which implies that
, which implies that
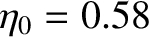 . Equations (D.58) and (D.60) then give
respectively. It turns out that these values for
. Equations (D.58) and (D.60) then give
respectively. It turns out that these values for  and
and 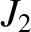 are fairly accurate [the true values are
are fairly accurate [the true values are
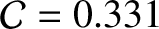 and
and
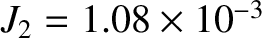 (Yoder 1995)]. This suggests that the response of the Earth to its centrifugal potential is essentially fluid-like, and, also, that the Earth's core is significantly denser than
its crust.
(Yoder 1995)]. This suggests that the response of the Earth to its centrifugal potential is essentially fluid-like, and, also, that the Earth's core is significantly denser than
its crust.
For the case of Jupiter (Yoder 1995),
These values are consistent with formula (D.59) provided
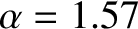 , which implies that
, which implies that
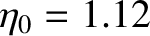 . Equations (D.58) and (D.60) then give
respectively. These values for
. Equations (D.58) and (D.60) then give
respectively. These values for  and
and 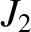 are somewhat inaccurate [the true values are
are somewhat inaccurate [the true values are
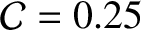 and
and
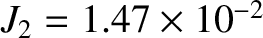 (Yoder 1995).] One possible reason for the disagrement is the fact that the values of
(Yoder 1995).] One possible reason for the disagrement is the fact that the values of 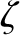 and
and
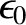 are
sufficiently large for Jupiter that it is not a good approximation to neglect terms that are second order in these quantities in the analysis (Cook 1980).
However, the fact that
are
sufficiently large for Jupiter that it is not a good approximation to neglect terms that are second order in these quantities in the analysis (Cook 1980).
However, the fact that 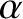 for Jupiter is significantly greater than
for Jupiter is significantly greater than 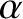 for the Earth suggests that the Jupiter's mass distribution is much more
centrally condensed than the Earth's.
for the Earth suggests that the Jupiter's mass distribution is much more
centrally condensed than the Earth's.
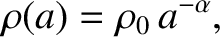
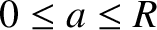 , where
, where
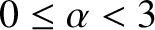 . Of course,
. Of course, 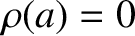 for
for 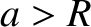 . According to Equations (D.26) and (D.42),
. According to Equations (D.26) and (D.42),
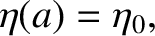
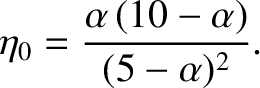
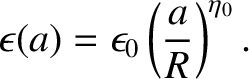
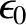
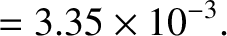
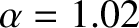 , which implies that
, which implies that
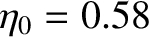 . Equations (D.58) and (D.60) then give
. Equations (D.58) and (D.60) then give

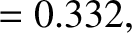
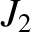
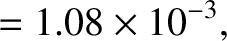
 and
and 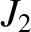 are fairly accurate [the true values are
are fairly accurate [the true values are
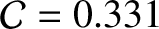 and
and
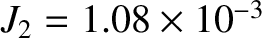 (Yoder 1995)]. This suggests that the response of the Earth to its centrifugal potential is essentially fluid-like, and, also, that the Earth's core is significantly denser than
its crust.
(Yoder 1995)]. This suggests that the response of the Earth to its centrifugal potential is essentially fluid-like, and, also, that the Earth's core is significantly denser than
its crust.
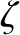
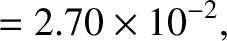
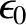
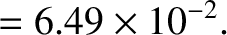
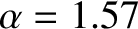 , which implies that
, which implies that
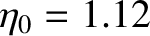 . Equations (D.58) and (D.60) then give
. Equations (D.58) and (D.60) then give

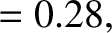
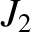
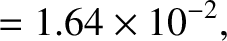
 and
and 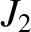 are somewhat inaccurate [the true values are
are somewhat inaccurate [the true values are
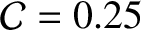 and
and
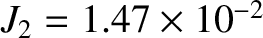 (Yoder 1995).] One possible reason for the disagrement is the fact that the values of
(Yoder 1995).] One possible reason for the disagrement is the fact that the values of 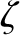 and
and
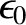 are
sufficiently large for Jupiter that it is not a good approximation to neglect terms that are second order in these quantities in the analysis (Cook 1980).
However, the fact that
are
sufficiently large for Jupiter that it is not a good approximation to neglect terms that are second order in these quantities in the analysis (Cook 1980).
However, the fact that 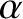 for Jupiter is significantly greater than
for Jupiter is significantly greater than 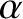 for the Earth suggests that the Jupiter's mass distribution is much more
centrally condensed than the Earth's.
for the Earth suggests that the Jupiter's mass distribution is much more
centrally condensed than the Earth's.