Combining Equations (D.2) and (D.3) with the previous three equations, we deduce that, to first order in
 , the total potential (i.e., the sum of the gravitational
and centrifugal potentials) can be written
, the total potential (i.e., the sum of the gravitational
and centrifugal potentials) can be written
 |
(D.22) |
where
Here, we have assumed that
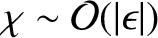 . However, according to Equation (D.7), if the rotating body is in hydrostatic equilibrium (in the
co-rotating frame) then
. However, according to Equation (D.7), if the rotating body is in hydrostatic equilibrium (in the
co-rotating frame) then 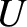 is a function of
is a function of  only. In other words,
only. In other words, 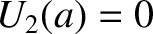 , which implies that
, which implies that
![$\displaystyle a^{\,2}\,\epsilon(a)\int_0^a \rho(a')\,a'^{\,2}\,da' -\frac{1}{5}...
...^\infty \rho(a')\,d[\epsilon(a')]
=\frac{{\mit\Omega}^{\,2}\,a^{\,5}}{8\pi\,G}.$](img4357.png) |
(D.24) |
Differentiation with respect to  yields
yields
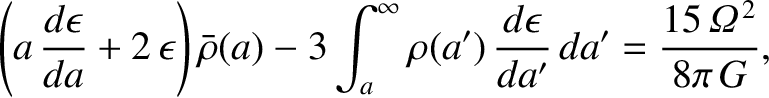 |
(D.25) |
where
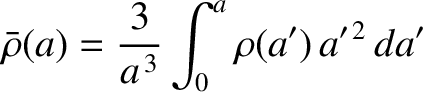 |
(D.26) |
is the mean density inside the spheroidal surface
![$r=a\,[1-(2/3)\,\epsilon(a)\,P_2(\cos\theta)]$](img4360.png) . Note that
. Note that
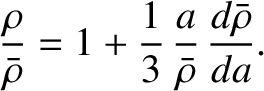 |
(D.27) |
Finally, differentiation of Equation (D.25) with respect to  gives
gives
 |
(D.28) |
This differential equation was first obtained by Clairaut in 1743 (Cook 1980).
Suppose that the outer boundary of the rotating body corresponds to 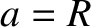 , where
, where 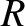 is the body's mean radius. [In other words,
is the body's mean radius. [In other words, 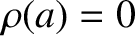 for
for 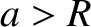 .] It follows that the
total mass of the body is
.] It follows that the
total mass of the body is
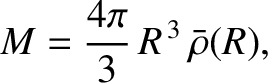 |
(D.29) |
The dimensionless parameter  , introduced in Section 6.5, is the typical ratio of the centrifugal acceleration to the gravitational
acceleration at
, introduced in Section 6.5, is the typical ratio of the centrifugal acceleration to the gravitational
acceleration at 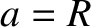 , and takes the form
, and takes the form
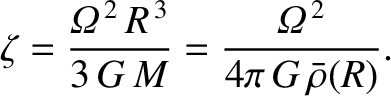 |
(D.30) |
Thus, it follows from Equation (D.25) that
 |
(D.31) |
Now, at an extremum of
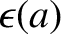 , we have
, we have
 . At such a point, Equation (D.28) yields
. At such a point, Equation (D.28) yields
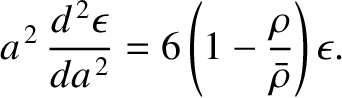 |
(D.32) |
However, if
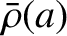 is a monotonically decreasing function of
is a monotonically decreasing function of  , as we would generally expect to be the case, then Equation (D.27)
reveals that
, as we would generally expect to be the case, then Equation (D.27)
reveals that
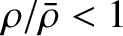 . Hence, the previous equation implies that, at the extremum,
. Hence, the previous equation implies that, at the extremum,
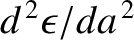 has the same sign as
has the same sign as 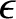 . In other words, the extremum is a minimum of
. In other words, the extremum is a minimum of
 . This implies that it is impossible to have a maximum of
. This implies that it is impossible to have a maximum of
 . Now, a Taylor expansion of Equation (D.27) about
. Now, a Taylor expansion of Equation (D.27) about 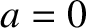 , assuming that
, assuming that
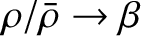 , where
, where
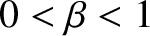 , reveals that
, reveals that
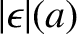 is an increasing function at small
is an increasing function at small  . We, thus, deduce that
. We, thus, deduce that
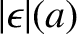 is
a monotonically increasing function. This implies that
is
a monotonically increasing function. This implies that
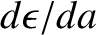 has the same sign as
has the same sign as 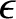 . Hence, Equation (D.31) reveals that
. Hence, Equation (D.31) reveals that
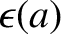 is everywhere positive. In other words, if
is everywhere positive. In other words, if
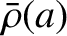 is a monotonically decreasing function then
is a monotonically decreasing function then
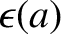 is necessarily a positive, monotonically
increasing function. Thus, we deduce that all density contours in the body are oblate spheroids.
is necessarily a positive, monotonically
increasing function. Thus, we deduce that all density contours in the body are oblate spheroids.
 , the total potential (i.e., the sum of the gravitational
and centrifugal potentials) can be written
, the total potential (i.e., the sum of the gravitational
and centrifugal potentials) can be written

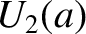
![$\displaystyle =-\frac{8\pi\,G}{3}\left\{\frac{\epsilon(a)}{a}\int_0^a \rho(a')\...
...2}\,da'-\frac{1}{5\,a^{\,3}}\int_0^a \rho(a')\,d[\epsilon(a')\,a'^{\,5}]\right.$](img4350.png)
![$\displaystyle \left.\phantom{=}-\frac{a^{\,2}}{5}\int_a^\infty
\rho(a')\,d[\epsilon(a')]\right\} +\frac{{\mit\Omega}^{\,2}\,a^{\,2}}{3}.$](img4354.png)
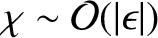 . However, according to Equation (D.7), if the rotating body is in hydrostatic equilibrium (in the
co-rotating frame) then
. However, according to Equation (D.7), if the rotating body is in hydrostatic equilibrium (in the
co-rotating frame) then 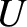 is a function of
is a function of  only. In other words,
only. In other words, 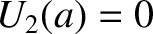 , which implies that
, which implies that
![$\displaystyle a^{\,2}\,\epsilon(a)\int_0^a \rho(a')\,a'^{\,2}\,da' -\frac{1}{5}...
...^\infty \rho(a')\,d[\epsilon(a')]
=\frac{{\mit\Omega}^{\,2}\,a^{\,5}}{8\pi\,G}.$](img4357.png)
 yields
where
is the mean density inside the spheroidal surface
yields
where
is the mean density inside the spheroidal surface
![$r=a\,[1-(2/3)\,\epsilon(a)\,P_2(\cos\theta)]$](img4360.png) . Note that
Finally, differentiation of Equation (D.25) with respect to
. Note that
Finally, differentiation of Equation (D.25) with respect to  gives
This differential equation was first obtained by Clairaut in 1743 (Cook 1980).
gives
This differential equation was first obtained by Clairaut in 1743 (Cook 1980).
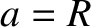 , where
, where 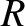 is the body's mean radius. [In other words,
is the body's mean radius. [In other words, 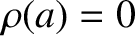 for
for 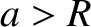 .] It follows that the
total mass of the body is
.] It follows that the
total mass of the body is
 , introduced in Section 6.5, is the typical ratio of the centrifugal acceleration to the gravitational
acceleration at
, introduced in Section 6.5, is the typical ratio of the centrifugal acceleration to the gravitational
acceleration at 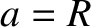 , and takes the form
, and takes the form
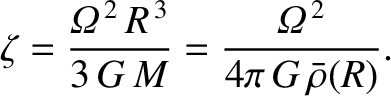
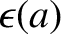 , we have
, we have
 . At such a point, Equation (D.28) yields
. At such a point, Equation (D.28) yields
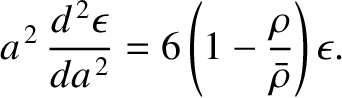
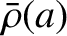 is a monotonically decreasing function of
is a monotonically decreasing function of  , as we would generally expect to be the case, then Equation (D.27)
reveals that
, as we would generally expect to be the case, then Equation (D.27)
reveals that
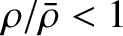 . Hence, the previous equation implies that, at the extremum,
. Hence, the previous equation implies that, at the extremum,
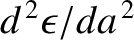 has the same sign as
has the same sign as 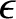 . In other words, the extremum is a minimum of
. In other words, the extremum is a minimum of
 . This implies that it is impossible to have a maximum of
. This implies that it is impossible to have a maximum of
 . Now, a Taylor expansion of Equation (D.27) about
. Now, a Taylor expansion of Equation (D.27) about 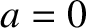 , assuming that
, assuming that
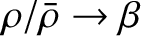 , where
, where
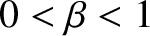 , reveals that
, reveals that
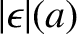 is an increasing function at small
is an increasing function at small  . We, thus, deduce that
. We, thus, deduce that
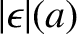 is
a monotonically increasing function. This implies that
is
a monotonically increasing function. This implies that
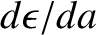 has the same sign as
has the same sign as 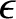 . Hence, Equation (D.31) reveals that
. Hence, Equation (D.31) reveals that
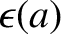 is everywhere positive. In other words, if
is everywhere positive. In other words, if
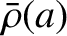 is a monotonically decreasing function then
is a monotonically decreasing function then
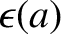 is necessarily a positive, monotonically
increasing function. Thus, we deduce that all density contours in the body are oblate spheroids.
is necessarily a positive, monotonically
increasing function. Thus, we deduce that all density contours in the body are oblate spheroids.