Next: Exercises Up: Lunar motion Previous: Regression of lunar ascending
 contributions
to
contributions
to 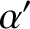 and
and 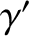 —see Equations (11.338) and (11.340), respectively—leading to the prediction
that the lunar perigee should precess at the same rate at which the ascending node regresses, and that both the perigee and
the node should complete full circuits around the Earth every
—see Equations (11.338) and (11.340), respectively—leading to the prediction
that the lunar perigee should precess at the same rate at which the ascending node regresses, and that both the perigee and
the node should complete full circuits around the Earth every 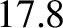 years (Taton and Wilson 1995). Of course, this prediction was
in serious disagreement with observations, according to which the lunar
perigee precesses at about twice the rate that the ascending node regresses. This discrepancy between theory
and observations lead Clairaut to briefly doubt the inverse-square nature of Newtonian gravity. Fortunately, Clairaut
realized in 1748 that the discrepancy could be resolved by carrying his expansion to higher order in
years (Taton and Wilson 1995). Of course, this prediction was
in serious disagreement with observations, according to which the lunar
perigee precesses at about twice the rate that the ascending node regresses. This discrepancy between theory
and observations lead Clairaut to briefly doubt the inverse-square nature of Newtonian gravity. Fortunately, Clairaut
realized in 1748 that the discrepancy could be resolved by carrying his expansion to higher order in  . Indeed, as is
clear from Equations (11.338) and (11.340), the
. Indeed, as is
clear from Equations (11.338) and (11.340), the
 contributions to
contributions to 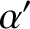 and
and 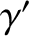 give rise to a significant increase in the precession rate of the lunar perigee relative to the regression rate of the
ascending node. In fact, the complete expression for
give rise to a significant increase in the precession rate of the lunar perigee relative to the regression rate of the
ascending node. In fact, the complete expression for 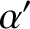 (Delaunay 1867, Hill 1894),
takes the form of a power series in
(Delaunay 1867, Hill 1894),
takes the form of a power series in  . Despite the fact that, for the case of the Moon,
. Despite the fact that, for the case of the Moon,  takes the relatively small value
takes the relatively small value  , this series only converges very slowly to the value
, this series only converges very slowly to the value
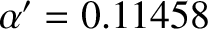 (Cook 1988), which corresponds to
a precession period (for a full circuit) of the Moon's perigee of
(Cook 1988), which corresponds to
a precession period (for a full circuit) of the Moon's perigee of
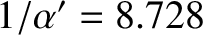 years. This estimate lies within 1 percent of the observed precession period
[i.e., 8.848 years (Yoder 1995)]. The residual disagreement between theory and observations is largely due to the neglect of small terms involving
years. This estimate lies within 1 percent of the observed precession period
[i.e., 8.848 years (Yoder 1995)]. The residual disagreement between theory and observations is largely due to the neglect of small terms involving 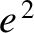 ,
, 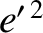 ,
,
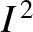 , and
, and 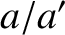 in the previous expression (Delaunay 1867).
The complete expression for
in the previous expression (Delaunay 1867).
The complete expression for 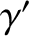 (Delaunay 1867),
also takes the form of a power series in
(Delaunay 1867),
also takes the form of a power series in  . Fortunately, for the case of the Moon, this series converges relatively quickly to the value
. Fortunately, for the case of the Moon, this series converges relatively quickly to the value
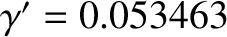 (Cook 1988), which corresponds to a regression period (for a full circuit) of the Moon's
ascending node of
(Cook 1988), which corresponds to a regression period (for a full circuit) of the Moon's
ascending node of
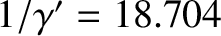 years. This estimate lies within half a percent of the observed regression period
[i.e., 18.615 years (Yoder 1995)].
Again, the residual disagreement between theory and observations is largely due to the neglect of small terms involving
years. This estimate lies within half a percent of the observed regression period
[i.e., 18.615 years (Yoder 1995)].
Again, the residual disagreement between theory and observations is largely due to the neglect of small terms involving 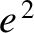 ,
, 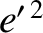 ,
,
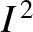 , and
, and 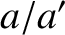 in the previous expression (Delaunay 1867).
The much faster convergence of series (11.342) compared to series (11.341)
accounts for the fact that our prediction for the regression period of the lunar ascending node is considerably more
accurate than that for the precession period of the perigee.
in the previous expression (Delaunay 1867).
The much faster convergence of series (11.342) compared to series (11.341)
accounts for the fact that our prediction for the regression period of the lunar ascending node is considerably more
accurate than that for the precession period of the perigee.