Next: Regression of lunar ascending Up: Lunar motion Previous: Summary of results
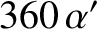 degrees per year. (Of course, a year corresponds to
degrees per year. (Of course, a year corresponds to
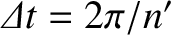 .) Furthermore, it is clear that this precession is entirely due to the perturbing influence of the Sun, because it depends only on the parameter
.) Furthermore, it is clear that this precession is entirely due to the perturbing influence of the Sun, because it depends only on the parameter  ,
which is a measure of this influence. Given that
,
which is a measure of this influence. Given that 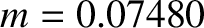 , we find that the perigee advances by
, we find that the perigee advances by
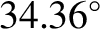 degrees per year. Hence, we predict that the perigee completes a full circuit about the Earth every
degrees per year. Hence, we predict that the perigee completes a full circuit about the Earth every
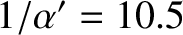 years.
In fact, the lunar perigee completes a full circuit every
years.
In fact, the lunar perigee completes a full circuit every 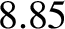 years. Our prediction is somewhat inaccurate because
our previous analysis neglected
years. Our prediction is somewhat inaccurate because
our previous analysis neglected
 , and smaller, contributions to the parameter
, and smaller, contributions to the parameter 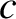 [see Equation (11.284)],
and these turn out to be significant. (See Section 11.17.)
[see Equation (11.284)],
and these turn out to be significant. (See Section 11.17.)