Next: Three-body problem Up: Rigid body rotation Previous: Cassini's laws
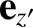 ,
,  , and
, and
 be the symmetry axis, the
angular momentum vector, and the angular velocity vector, respectively, of a rotating body with an axis of symmetry.
Demonstrate that these three vectors are coplanar.
be the symmetry axis, the
angular momentum vector, and the angular velocity vector, respectively, of a rotating body with an axis of symmetry.
Demonstrate that these three vectors are coplanar.
 is the angle between the symmetry axis and the instantaneous axis of
rotation, show that the angle between the axis of rotation and the invariable line
(the
is the angle between the symmetry axis and the instantaneous axis of
rotation, show that the angle between the axis of rotation and the invariable line
(the 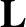 vector) is
vector) is
![$\displaystyle \tan^{-1}\left[\frac{({\cal I}_\parallel-{\cal I}_\perp)\,\tan\alpha}{{\cal I}_\parallel+{\cal I}_\perp\,\tan^2\alpha}\right]
$](img2077.png)
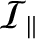 (the moment of inertia about the symmetry axis) is greater than
(the moment of inertia about the symmetry axis) is greater than
 (the moment of inertia about an axis normal to the symmetry axis). (From Fowles and Cassiday 2005.)
(the moment of inertia about an axis normal to the symmetry axis). (From Fowles and Cassiday 2005.)
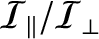 is 2 (symmetrical lamina) show
from the previous result that the angle between the angular velocity and angular momentum
vectors cannot exceed
is 2 (symmetrical lamina) show
from the previous result that the angle between the angular velocity and angular momentum
vectors cannot exceed
 . Find the corresponding
value of
. Find the corresponding
value of  . (Modified from Fowles and Cassiday 2005.)
. (Modified from Fowles and Cassiday 2005.)
 and mass
and mass  is constrained to rotate
with constant angular velocity
is constrained to rotate
with constant angular velocity  about an axis passing through the
center of the rod, and making an angle
about an axis passing through the
center of the rod, and making an angle  with the rod.
Show that the angular momentum about the center of the rod is perpendicular to the rod, and is of magnitude
with the rod.
Show that the angular momentum about the center of the rod is perpendicular to the rod, and is of magnitude
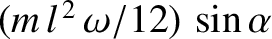 . Show that
the torque is perpendicular to both the rod and the angular momentum vector,
and is of magnitude
. Show that
the torque is perpendicular to both the rod and the angular momentum vector,
and is of magnitude
 . (From Fowles and Cassiday 2005.)
. (From Fowles and Cassiday 2005.)
 and mass
and mass  is constrained to rotate
with constant angular velocity
is constrained to rotate
with constant angular velocity  about an axis passing through its center, and making an angle
about an axis passing through its center, and making an angle  with the normal to the disk.
Find the angular momentum about the center of the disk, as
well as the torque acting on the disk.
with the normal to the disk.
Find the angular momentum about the center of the disk, as
well as the torque acting on the disk.
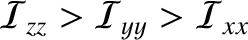 .
.
 ) when the body rotates about the
) when the body rotates about the  - and the
- and the  -axes, respectively.
-axes, respectively.
 -axis or the
-axis or the  -axis, but unstable when it rotates about the
-axis, but unstable when it rotates about the  -axis.
-axis.
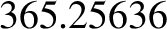 days (Yoder 1995). The mean tropical year is defined as the
average time interval between successive vernal equinoxes. Demonstrate that, as a consequence of the precession of the equinoxes, whose period
is 25,772 years (Yoder 1995), the length of the mean tropical year is
days (Yoder 1995). The mean tropical year is defined as the
average time interval between successive vernal equinoxes. Demonstrate that, as a consequence of the precession of the equinoxes, whose period
is 25,772 years (Yoder 1995), the length of the mean tropical year is 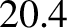 minutes shorter than that of the mean sidereal year (i.e.,
minutes shorter than that of the mean sidereal year (i.e., 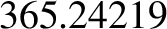 days).
days).
 about the Earth. Suppose that the normal to the plane of the orbit subtends
an angle
about the Earth. Suppose that the normal to the plane of the orbit subtends
an angle  with the Earth's axis of rotation. By approximating the
orbiting satellite as a uniform ring, demonstrate that the Earth's oblateness causes
the plane of the satellite's orbit to precess about the Earth's rotational
axis at the approximate rate
with the Earth's axis of rotation. By approximating the
orbiting satellite as a uniform ring, demonstrate that the Earth's oblateness causes
the plane of the satellite's orbit to precess about the Earth's rotational
axis at the approximate rate

 is the satellite's orbital angular velocity,
is the satellite's orbital angular velocity,  is the Earth's mean radius,
is the Earth's mean radius,
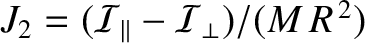 ,
,  is the Earth's mass, and
is the Earth's mass, and
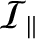 and
and
 are the Earth's parallel and perpendicular (to the rotation axis) moments of inertia. Is the precession in the same sense as the orbital motion, or the
opposite sense?
are the Earth's parallel and perpendicular (to the rotation axis) moments of inertia. Is the precession in the same sense as the orbital motion, or the
opposite sense?
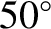 N and
N and 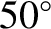 S? Is the
direction of the satellite orbit in the same sense as the Earth's rotation (prograde),
or the opposite sense (retrograde)? Note that
S? Is the
direction of the satellite orbit in the same sense as the Earth's rotation (prograde),
or the opposite sense (retrograde)? Note that
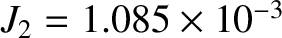 for the Earth (Yoder 1995).
for the Earth (Yoder 1995).
 :
: spin-orbit resonance. Demonstrate that, to lowest order in the eccentricity,
the optical libration of the moon can be accounted for by saying that the moon's long axis (in the orbital plane) always
points toward the empty focus of the orbit.
spin-orbit resonance. Demonstrate that, to lowest order in the eccentricity,
the optical libration of the moon can be accounted for by saying that the moon's long axis (in the orbital plane) always
points toward the empty focus of the orbit.