Let
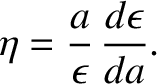 |
(D.33) |
It follows that
Equation (D.28) transforms into
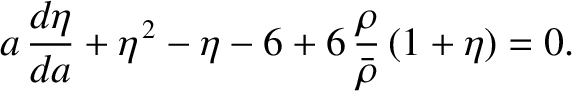 |
(D.36) |
Making use of Equation (D.27), this reduces to
 |
(D.37) |
However, it is easily demonstrated that
![$\displaystyle \frac{\left.d\left[\bar{\rho}\,a^{\,5}\,(1+\eta)^{1/2}\right]\rig...
...}\,\frac{d\bar{\rho}}{da}+\frac{5}{a}
+\frac{1}{2\,(1+\eta)}\,\frac{d\eta}{da}.$](img4386.png) |
(D.38) |
Hence, Equation (D.37) yields Radau's equation (Radau 1885),
![$\displaystyle \frac{d}{da}\left[\bar{\rho}\,a^{\,5}\,(1+\eta)^{1/2}\right] = 5\,\bar{\rho}\,a^{\,4}\,\psi(\eta),$](img4387.png) |
(D.39) |
where
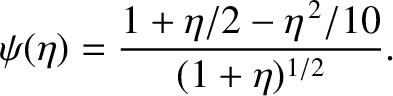 |
(D.40) |
Figure: D.1
The function
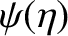 .
.
|
|
Figure D.1 shows the function
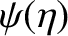 . It should be noted that
. It should be noted that 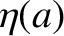 is necessarily positive, because
is necessarily positive, because
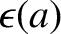 is a monotonically increasing function. Moreover,
is a monotonically increasing function. Moreover, 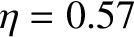 on the surface of the Earth, and the largest value of
on the surface of the Earth, and the largest value of 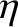 for any planet in the solar system is about
for any planet in the solar system is about 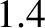 (Cook 1980). It is thus clear, from the figure, that it is an excellent approximation to take
(Cook 1980). It is thus clear, from the figure, that it is an excellent approximation to take
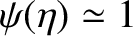 for such bodies. This leads to the
so-called reduced Radau equation,
for such bodies. This leads to the
so-called reduced Radau equation,
![$\displaystyle \frac{d}{da}\left[\bar{\rho}\,a^{\,5}\,(1+\eta)^{1/2}\right] \simeq 5\,\bar{\rho}\,a^{\,4},$](img4394.png) |
(D.41) |
which can immediately be integrated to give
 |
(D.42) |


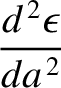
![$\displaystyle =\left[\frac{1}{a}\,\frac{d\eta}{da}+\frac{\eta\,(\eta-1)}{a^{\,2}}\right].$](img4383.png)
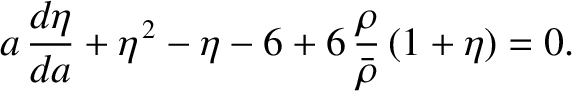
![$\displaystyle \frac{\left.d\left[\bar{\rho}\,a^{\,5}\,(1+\eta)^{1/2}\right]\rig...
...}\,\frac{d\bar{\rho}}{da}+\frac{5}{a}
+\frac{1}{2\,(1+\eta)}\,\frac{d\eta}{da}.$](img4386.png)
![$\displaystyle \frac{d}{da}\left[\bar{\rho}\,a^{\,5}\,(1+\eta)^{1/2}\right] = 5\,\bar{\rho}\,a^{\,4}\,\psi(\eta),$](img4387.png)
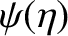 . It should be noted that
. It should be noted that 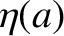 is necessarily positive, because
is necessarily positive, because
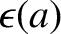 is a monotonically increasing function. Moreover,
is a monotonically increasing function. Moreover, 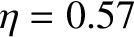 on the surface of the Earth, and the largest value of
on the surface of the Earth, and the largest value of 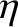 for any planet in the solar system is about
for any planet in the solar system is about 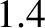 (Cook 1980). It is thus clear, from the figure, that it is an excellent approximation to take
(Cook 1980). It is thus clear, from the figure, that it is an excellent approximation to take
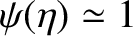 for such bodies. This leads to the
so-called reduced Radau equation,
for such bodies. This leads to the
so-called reduced Radau equation,
![$\displaystyle \frac{d}{da}\left[\bar{\rho}\,a^{\,5}\,(1+\eta)^{1/2}\right] \simeq 5\,\bar{\rho}\,a^{\,4},$](img4394.png)