Next: Calculation of gravitational potential Up: Darwin-Radau equation Previous: Darwin-Radau equation
 ,
,  ,
,  are spherical coordinates whose symmetry axis coincides with the axis of rotation.
Moreover,
are spherical coordinates whose symmetry axis coincides with the axis of rotation.
Moreover, 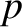 is the fluid pressure,
is the fluid pressure, 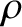 the mass density,
the mass density,
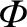 the gravitational potential,
the gravitational potential, 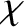 the centrifugal
potential, and
the centrifugal
potential, and
 the angular rotation velocity.
Taking the curl of Equation (D.1), we
deduce that
the angular rotation velocity.
Taking the curl of Equation (D.1), we
deduce that
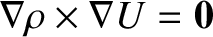 , and, hence, that
Let us assume that the contours of
, and, hence, that
Let us assume that the contours of 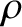 are spheroidal, so that
where
Here,
are spheroidal, so that
where
Here,  and
and
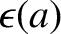 are the mean radius and ellipticity of the density contour
are the mean radius and ellipticity of the density contour
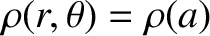 , respectively. Furthermore, it is assumed that
, respectively. Furthermore, it is assumed that
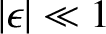 .
(See Section 3.6).
It follows from Equations (D.4) and (D.5) that
The aim of this appendix is to deduce
the relationship between the degree of flattening of the body, its rotational angular velocity, and its
moment of inertia about its rotation axis.
.
(See Section 3.6).
It follows from Equations (D.4) and (D.5) that
The aim of this appendix is to deduce
the relationship between the degree of flattening of the body, its rotational angular velocity, and its
moment of inertia about its rotation axis.