Next: Gravitational potential Up: Newtonian gravity Previous: Newtonian gravity
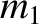 and
and 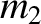 that are located at position vectors
that are located at position vectors 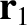 and
and 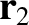 ,
respectively. The gravitational force
,
respectively. The gravitational force
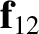 that mass
that mass 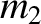 exerts on mass
exerts on mass 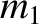 is written
The gravitational force
is written
The gravitational force
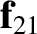 that mass
that mass 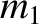 exerts on mass
exerts on mass 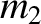 is equal and opposite; that is,
is equal and opposite; that is,
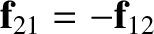 .
See Figure 2.3.
Here, the constant of proportionality,
.
See Figure 2.3.
Here, the constant of proportionality, 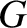 , is called the universal gravitational constant
and takes the value (Yoder 1995)
, is called the universal gravitational constant
and takes the value (Yoder 1995)
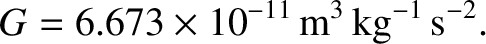 |
(3.2) |
Incidentally, there is something rather curious about Equation (3.1). According to this law, the gravitational force acting on a given object is directly proportional to that object's inertial mass. Why, though, should inertia be related to the force of gravity? After all, inertia simply measures the reluctance of a given body to deviate from its preferred state of uniform motion in a straight line, in response to some external force. The preceding question perplexed physicists for many years, but was eventually answered when Albert Einstein published his general theory of relativity in 1916. According to Einstein, inertial mass acts as a sort of gravitational charge because it is impossible to distinguish an acceleration produced by a gravitational field from an apparent acceleration generated by observing motion in a non-inertial reference frame. The assumption that these two types of acceleration are indistinguishable leads directly to all of the strange predictions of general relativity; for instance, clocks in different gravitational potentials run at different rates, mass bends space, and so on (Rindler 1977).