| (5.105) |
| (5.105) |
| (5.106) |
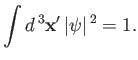 |
(5.107) |
This is all very familiar. However, we now know how to generalize this scheme
to deal with a spin one-half particle. Instead of representing the
state of the particle by a single wavefunction, we use two wavefunctions.
The first,
![]() , specifies the probability density of
observing the particle at position
, specifies the probability density of
observing the particle at position ![]() with spin angular momentum
with spin angular momentum ![]() in the
in the ![]() -direction. The second,
-direction. The second,
![]() , specifies the
probability density of
observing the particle at position
, specifies the
probability density of
observing the particle at position ![]() with spin angular momentum
with spin angular momentum ![]() in the
in the ![]() -direction. In the Pauli scheme, these wavefunctions
are combined into a spinor-wavefunction,
-direction. In the Pauli scheme, these wavefunctions
are combined into a spinor-wavefunction, ![]() , which is simply the column vector of
, which is simply the column vector of ![]() and
and ![]() .
In general, the Hamiltonian is a function of the position, momentum, and spin
operators. Adopting the Schrödinger representation, and the Pauli scheme,
the energy eigenvalue problem reduces to
.
In general, the Hamiltonian is a function of the position, momentum, and spin
operators. Adopting the Schrödinger representation, and the Pauli scheme,
the energy eigenvalue problem reduces to
Suppose that the Hamiltonian has no dependence on the spin operators. In this
case, the Hamiltonian is represented as diagonal ![]() matrix partial
differential operator in the Schrödinger/Pauli scheme. [See Equation (5.91).]
In other words, the partial differential equation for
matrix partial
differential operator in the Schrödinger/Pauli scheme. [See Equation (5.91).]
In other words, the partial differential equation for ![]() decouples
from that for
decouples
from that for ![]() . In fact, both equations have the same form, so there
is really only one differential equation. In this
situation, the most general solution to Equation (5.108) can be written in the
factorized form
. In fact, both equations have the same form, so there
is really only one differential equation. In this
situation, the most general solution to Equation (5.108) can be written in the
factorized form
Suppose that the Hamiltonian depends only on the spin operators. In this
case, the Hamiltonian is represented as a ![]() matrix of complex numbers
in the Schrödinger/Pauli scheme [see Equation (5.74)], and the spinor eigenvalue
equation (5.108) reduces to a straightforward matrix eigenvalue problem.
The most general solution can again be written in the factorized form
matrix of complex numbers
in the Schrödinger/Pauli scheme [see Equation (5.74)], and the spinor eigenvalue
equation (5.108) reduces to a straightforward matrix eigenvalue problem.
The most general solution can again be written in the factorized form
In general, of course, the Hamiltonian is a function of both position and
spin operators. In this case, it is not possible to factorize the
spinor-wavefunction as in Equations (5.109) and (5.110).
In other words, a general Hamiltonian causes the
direction of the particle's spin angular momentum to vary with position in
some specified manner. This can only be represented as a spinor-wavefunction involving
different wavefunctions, ![]() and
and ![]() .
.