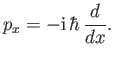Next: Generalized Schrödinger Representation
Up: Position and Momentum
Previous: Wavefunctions
Schrödinger Representation
Consider the simple system described in the previous section. A general
state ket can be written
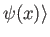 , where
, where 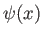 is a general function of
the position operator
is a general function of
the position operator 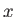 , and
, and 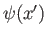 is the associated wavefunction.
Consider the ket whose wavefunction is
is the associated wavefunction.
Consider the ket whose wavefunction is
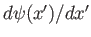 . This ket is
denoted
. This ket is
denoted
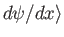 . The new ket is clearly a linear function of
the original ket, so we can think of it as the result of some linear
operator acting on
. The new ket is clearly a linear function of
the original ket, so we can think of it as the result of some linear
operator acting on
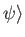 . Let us denote this operator
. Let us denote this operator
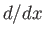 . It follows that
. It follows that
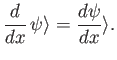 |
(2.37) |
Any linear operator that acts on ket vectors can also act on bra vectors.
Consider 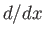 acting on a general bra
acting on a general bra
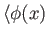 . According to
Equation (1.37), the bra
. According to
Equation (1.37), the bra
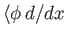 satisfies
satisfies
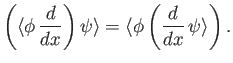 |
(2.38) |
Making use of Equations (2.27), (2.29), and (2.37) we can write
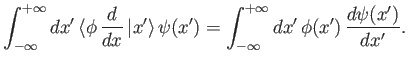 |
(2.39) |
The right-hand side can be transformed via integration by parts to give
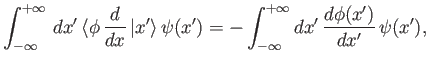 |
(2.40) |
assuming that the contributions from the limits of integration vanish.
It follows that
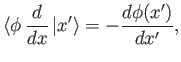 |
(2.41) |
which implies that
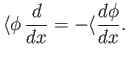 |
(2.42) |
The neglect of contributions from the limits of integration in Equation (2.40) is
reasonable because
physical wavefunctions are square-integrable. [See Equation (2.31).]
Note that
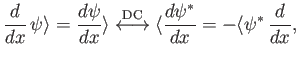 |
(2.43) |
where use has been made of Equation (2.42).
It follows, by comparison with Equations (1.38) and (2.36), that
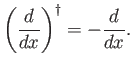 |
(2.44) |
Thus, 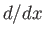 is an anti-Hermitian operator.
is an anti-Hermitian operator.
Let us evaluate the commutation relation between the operators 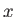 and
and 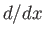 .
We have
.
We have
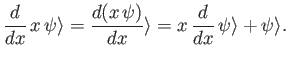 |
(2.45) |
Because this holds for any ket
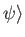 , it follows that
, it follows that
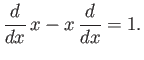 |
(2.46) |
Let 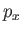 be the momentum conjugate to
be the momentum conjugate to 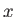 (for the simple system under consideration,
(for the simple system under consideration,
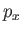 is a straightforward linear momentum). According to Equation (2.25),
is a straightforward linear momentum). According to Equation (2.25),
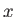 and
and 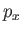 satisfy the commutation relation
satisfy the commutation relation
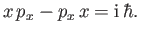 |
(2.47) |
It can be seen, by comparison with Equation (2.46), that
the Hermitian operator
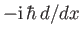 satisfies the same commutation relation with
satisfies the same commutation relation with 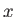 that
that 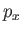 does.
The most general conclusion which may be drawn from a comparison of Equations (2.46)
and (2.47) is that
does.
The most general conclusion which may be drawn from a comparison of Equations (2.46)
and (2.47) is that
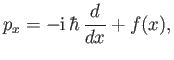 |
(2.48) |
because (as is easily demonstrated) a general function 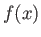 of the position
operator automatically commutes with
of the position
operator automatically commutes with 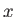 . (See Exercise 3.)
. (See Exercise 3.)
We have chosen to normalize the eigenkets and
eigenbras of the position operator such that they satisfy
the normalization condition (2.26). However, this choice of normalization does not
uniquely determine the eigenkets and
eigenbras. Suppose that we transform to a new
set of eigenbras which are related to the old set via
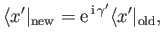 |
(2.49) |
where
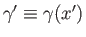 is a real function of
is a real function of 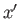 .
This transformation amounts to a rearrangement of the relative
phases of the eigenbras. The new
normalization condition is
.
This transformation amounts to a rearrangement of the relative
phases of the eigenbras. The new
normalization condition is
Thus, the new eigenbras satisfy the same normalization condition
as the old eigenbras.
By definition, the standard ket 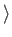 satisfies
satisfies
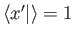 .
It follows from Equation (2.49) that the new standard ket is related to the
old standard ket via
.
It follows from Equation (2.49) that the new standard ket is related to the
old standard ket via
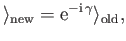 |
(2.51) |
where
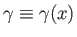 is a real function of the position operator
is a real function of the position operator 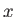 .
The dual of the previous equation yields the transformation rule for
the standard bra,
.
The dual of the previous equation yields the transformation rule for
the standard bra,
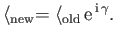 |
(2.52) |
The transformation rule for a general operator 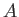 follows from Equations (2.51) and (2.52),
plus the requirement that the triple product
follows from Equations (2.51) and (2.52),
plus the requirement that the triple product
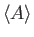 remain
invariant (which must be the case, otherwise the probability of a measurement
yielding a certain result would depend on the choice of eigenbras). Thus,
remain
invariant (which must be the case, otherwise the probability of a measurement
yielding a certain result would depend on the choice of eigenbras). Thus,
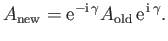 |
(2.53) |
Of course, if 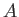 commutes with
commutes with 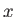 then
then 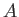 is invariant under the transformation.
In fact,
is invariant under the transformation.
In fact, 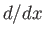 is the only operator (that we know of) that does not commute
with
is the only operator (that we know of) that does not commute
with 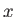 , so Equation (2.53) yields
, so Equation (2.53) yields
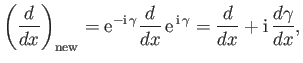 |
(2.54) |
where the subscript ``old'' is taken as read. It follows, from Equation (2.48), that
the momentum operator 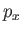 can be written
can be written
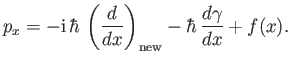 |
(2.55) |
Thus, the special choice
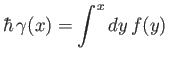 |
(2.56) |
yields
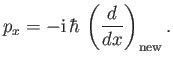 |
(2.57) |
Equation (2.56) fixes 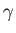 to
within an arbitrary additive constant. In other words, the special eigenkets and eigenbras
for which Equation (2.57) is true are determined to within an arbitrary common phase-factor.
to
within an arbitrary additive constant. In other words, the special eigenkets and eigenbras
for which Equation (2.57) is true are determined to within an arbitrary common phase-factor.
In conclusion, it is possible to find a set of basis eigenkets and eigenbras
of the position operator 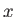 that satisfy the normalization condition (2.26),
and for which the momentum conjugate to
that satisfy the normalization condition (2.26),
and for which the momentum conjugate to 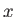 can be represented as the operator
can be represented as the operator
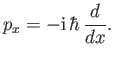 |
(2.58) |
A general state ket is written
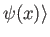 , where the standard ket
, where the standard ket 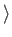 satisfies
satisfies
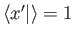 , and where
, and where
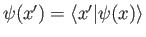 is the wavefunction.
This scheme is known as the Schrödinger representation, and is the
basis of wave mechanics.
is the wavefunction.
This scheme is known as the Schrödinger representation, and is the
basis of wave mechanics.



Next: Generalized Schrödinger Representation
Up: Position and Momentum
Previous: Wavefunctions
Richard Fitzpatrick
2016-01-22
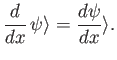
![]() acting on a general bra
acting on a general bra
![]() . According to
Equation (1.37), the bra
. According to
Equation (1.37), the bra
![]() satisfies
satisfies
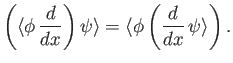
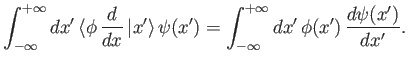
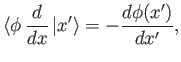
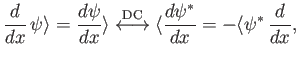
![]() and
and ![]() .
We have
.
We have
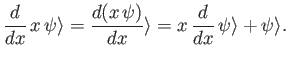
![]() satisfies
satisfies
![]() .
It follows from Equation (2.49) that the new standard ket is related to the
old standard ket via
.
It follows from Equation (2.49) that the new standard ket is related to the
old standard ket via
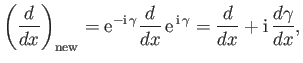
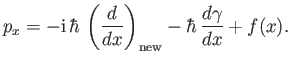
![]() that satisfy the normalization condition (2.26),
and for which the momentum conjugate to
that satisfy the normalization condition (2.26),
and for which the momentum conjugate to ![]() can be represented as the operator
can be represented as the operator