Kepler's Laws

As is well known, Johannes Kepler was the first astronomer to correctly describe planetary motion in the solar system (in works published between 1609 and 1619). The motion of the planets is summed up in three simple laws:

1. The planetary orbits are all ellipses that are confocal with the Sun (i.e., the Sun lies at one of the focii of each ellipse).
2. The radius vectors connecting each planet to the Sun sweep out equal areas in equal time intervals.
3. The squares of the orbital periods of the planets are proportional to the cubes of their orbital major radii.

Let us now see if we can derive Kepler's laws from Newton's laws of motion.

Suppose that the Sun, which is of mass $M$, is located at the origin of our coordinate system. Consider a planet, of mass $m$, whose instantaneous displacement is ${\bf r}$. The gravitational force exerted on the planet by the Sun is thus written

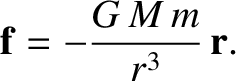$${\bf f} = - \frac{G\,M\,m}{r^{3}}\,{\bf r}.$$ (1.275)

[See Equation (1.257).] An equal and opposite force to (1.275) acts on the Sun. However, we shall assume that the Sun is so much more massive than the planet in question that this force does not cause the Sun's position to shift appreciably. Hence, the Sun will always remain at the origin of our coordinate system. Likewise, we shall neglect the gravitational forces exerted on our planet by the other planets in the solar system, compared to the much larger gravitational force exerted by the Sun. Thus, according to Newton's second law, the equation of motion of our planet is

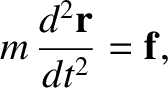$$m\,\frac{d^2{\bf r}}{dt^2} = {\bf f},$$ (1.276)

which reduces to

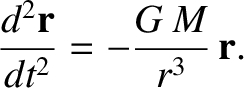$$\frac{d^2{\bf r}}{dt^2}= -\frac{G\,M}{r^{3}}\,{\bf r}.$$ (1.277)

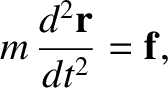
Note that the planetary mass, $m$, has cancelled out on both sides of the previous equation.