Next: Scalar Triple Product Up: Vector Algebra and Vector Previous: Vector Product
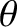 whose magnitude
is the angle of the rotation,
whose magnitude
is the angle of the rotation, 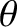 , and whose direction is parallel to the axis of
rotation, in the sense determined by a right-hand circulation rule. Unfortunately, this is not a good vector. The problem is that the addition of rotations
is not commutative, whereas vector addition is commuative.
Figure A.11 shows the effect of applying two successive
, and whose direction is parallel to the axis of
rotation, in the sense determined by a right-hand circulation rule. Unfortunately, this is not a good vector. The problem is that the addition of rotations
is not commutative, whereas vector addition is commuative.
Figure A.11 shows the effect of applying two successive 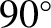 rotations,
one about
rotations,
one about 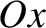 , and the other about the
, and the other about the 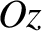 , to a standard six-sided die. In the
left-hand case, the
, to a standard six-sided die. In the
left-hand case, the 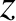 -rotation is applied before the
-rotation is applied before the 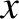 -rotation, and vice
versa in the right-hand case. It can be seen that the die ends up in two completely
different states. In other words, the
-rotation, and vice
versa in the right-hand case. It can be seen that the die ends up in two completely
different states. In other words, the 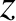 -rotation plus the
-rotation plus the
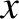 -rotation does not equal
the
-rotation does not equal
the 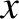 -rotation plus the
-rotation plus the 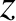 -rotation. This non-commuting algebra cannot be
represented by vectors. So, although rotations have a well-defined magnitude and
direction, they are not vector quantities.
-rotation. This non-commuting algebra cannot be
represented by vectors. So, although rotations have a well-defined magnitude and
direction, they are not vector quantities.
But, this is not quite the end of the story. Suppose that we take a general vector
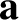 and rotate it about
and rotate it about 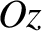 by a small angle
by a small angle
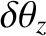 .
This is equivalent to rotating the coordinate axes about the
.
This is equivalent to rotating the coordinate axes about the 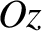 by
by
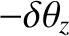 .
According to Equations (A.20)–(A.22), we have
.
According to Equations (A.20)–(A.22), we have
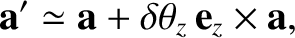 |
(1.48) |
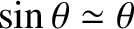 and
and
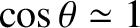 . The previous equation can easily be generalized to allow
small rotations about
. The previous equation can easily be generalized to allow
small rotations about 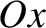 and
and 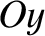 by
by
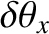 and
and
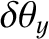 ,
respectively. We find that
where
,
respectively. We find that
where
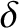 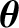 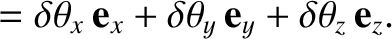 |
(1.50) |
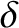
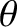 , but it only
works for small angle rotations (i.e., sufficiently small that the small-angle approximations of sine and cosine are good). According to the previous equation,
a small
, but it only
works for small angle rotations (i.e., sufficiently small that the small-angle approximations of sine and cosine are good). According to the previous equation,
a small 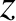 -rotation plus a small
-rotation plus a small 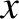 -rotation is (approximately) equal to
the two rotations applied in the opposite order.
The fact that infinitesimal rotation is a vector implies that angular velocity,
-rotation is (approximately) equal to
the two rotations applied in the opposite order.
The fact that infinitesimal rotation is a vector implies that angular velocity,
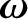 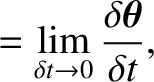 |
(1.51) |
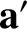 is interpreted as
is interpreted as
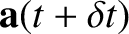 in Equation (A.49) then it follows that the equation of motion of a vector
that precesses about the origin with some angular velocity
in Equation (A.49) then it follows that the equation of motion of a vector
that precesses about the origin with some angular velocity 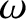 is
is