Next: Helium Diffraction Up: Experimental Basis of Quantum Previous: Double-Slit Interference of Light
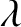 , or, alternatively, the wavenumber,
, or, alternatively, the wavenumber,
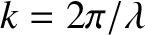 , can be deduced from the spacing
of the maxima in the interference pattern.
Thomson, Davisson, and Germer found that the momentum,
, can be deduced from the spacing
of the maxima in the interference pattern.
Thomson, Davisson, and Germer found that the momentum,  , of an electron is related to its wavevector,
, of an electron is related to its wavevector,  , according to the
following
simple relation:
The associated wavelength,
, according to the
following
simple relation:
The associated wavelength,
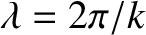 , is known as the de Broglie wavelength, because the previous relation was first hypothesized by Louis de Broglie in 1926. (See Section 4.1.9.)
, is known as the de Broglie wavelength, because the previous relation was first hypothesized by Louis de Broglie in 1926. (See Section 4.1.9.)
It turns out that wave-particle duality only manifests itself on lengthscales less than, or of order, the de Broglie wavelength. Under normal circumstances, this wavelength is fairly small. For instance, the de Broglie wavelength of an electron is
![$\displaystyle \lambda_e = 1.2\times 10^{-9}\,[E({\rm eV})]^{-1/2}\,{\rm m},$](img2883.png) |
(4.6) |
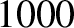 V
acquires an energy of
V
acquires an energy of 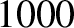 eV, and so on. Electrons in atoms typically have energies in the range
eV, and so on. Electrons in atoms typically have energies in the range 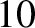 to
to 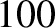 eV.)
eV.)