Next: Double-Slit Interference of Light Up: Experimental Basis of Quantum Previous: Compton Scattering
Consider the following well-known experiment. A beam of plane polarized
light is passed through a thin polarizing film whose plane is normal to the beam's direction of propagation, and which
has the property that it is only transparent to
light whose direction of polarization lies perpendicular to its optic axis (which is assumed to lie in the plane
of the film).
Classical electromagnetic wave theory tells us that
if the beam is polarized perpendicular to the optic axis then all of the light
is transmitted, if the beam is polarized parallel to the optic axis
then none of the light is transmitted, and if the light is
polarized at an angle 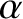 to the axis then a fraction
to the axis then a fraction
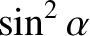 of the beam energy is transmitted; the latter result is known as Malus's law,
after Étienne-Louis Malus who discovered it in 1808. Let us try to account for these observations
at the individual photon level.
of the beam energy is transmitted; the latter result is known as Malus's law,
after Étienne-Louis Malus who discovered it in 1808. Let us try to account for these observations
at the individual photon level.
A beam of light that is plane polarized in a certain direction is presumably made up of a stream of photons that are each plane polarized in that direction. This picture leads to no difficulty if the direction of polarization lies parallel or perpendicular to the optic axis of the polarizing film. In the former case, none of the photons are transmitted, and, in the latter case, all of the photons are transmitted. But, what happens in the case of an obliquely polarized incident beam?
The previous question is not very precise. Let us reformulate it as a question
relating to the result of some experiment that we could perform.
Suppose that we were to fire a single photon at a polarizing film, and then look
to see whether or not it emerges on the other side. The possible
results of the experiment are that either a whole photon (whose energy
is equal to the energy of the incident photon) is observed, or no photon
is observed. Any photon that is transmitted though the film must
be polarized perpendicular to the film's optic axis. Furthermore, it is impossible to
imagine (in physics) finding part of a photon on the other side of the film.
If we repeat the experiment a great number of times then, on average,
a fraction
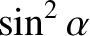 of the photons are transmitted through the film, and
a fraction
of the photons are transmitted through the film, and
a fraction
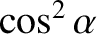 are absorbed. Thus, given that the trials are statistically independent of one another, we must conclude that an individual photon has a probability
are absorbed. Thus, given that the trials are statistically independent of one another, we must conclude that an individual photon has a probability
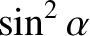 of being transmitted as a photon polarized in the plane
perpendicular to the optic axis, and a probability
of being transmitted as a photon polarized in the plane
perpendicular to the optic axis, and a probability
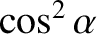 of
being absorbed. These values for the probabilities lead to the correct classical
limit for a beam containing a large number of photons.
of
being absorbed. These values for the probabilities lead to the correct classical
limit for a beam containing a large number of photons.
Note that we have only been able to preserve the individuality of photons, in all cases, by abandoning the determinacy of classical theory, and adopting a fundamentally probabilistic approach. We have no way of knowing whether a given obliquely-polarized photon is going to be absorbed by, or transmitted through, the polarizing film. We only know the probability of each event occurring. This is a fairly sweeping statement. Recall, however, that the state of a photon is fully specified once its energy, direction of propagation, and polarization are known. If we imagine performing experiments using monochromatic light, normally incident on a polarizing film, with a particular oblique polarization, then the state of each individual photon in the beam is completely specified, and nothing remains to uniquely determine whether the photon is transmitted or absorbed by the film.
The previous discussion about the possible results of an experiment with a single obliquely polarized photon incident on a polarizing film answers all that can be legitimately asked about what happens to the photon when it reaches the film. Questions as to what determines whether the photon is transmitted or not, or how it changes its direction of polarization, are illegitimate, because they do not relate to the outcome of a possible experiment. Nevertheless, some further description is needed, in order to allow the results of this experiment to be correlated with the results of other experiments that can be performed using photons.
The further description provided by quantum mechanics is as follows. It is supposed that a photon polarized obliquely to the optic axis can be regarded as being partly in a state of polarization parallel to the axis, and partly in a state of polarization perpendicular to the axis. In other words, the oblique polarization state is some sort of superposition of two states of parallel and perpendicular polarization. Because there is nothing special about the orientation of the optic axis in our experiment, we deduce that any photon polarization state can be regarded as a superposition of two mutually perpendicular polarization states. (Recall, from Section 2.4.4, that there are only two independent polarizations of an electromagnetic wave.) When we cause a photon to encounter a polarizing film, we are subjecting it to an observation. In fact, we are observing whether it is polarized parallel or perpendicular to the film's optic axis. The effect of making this observation is to force the photon entirely into a state of parallel or perpendicular polarization. In other words, the photon has to jump suddenly from being partly in each of these two states to being entirely in one or the other of them. Which of the two states it will jump into cannot be predicted, but is governed by probability laws. If the photon jumps into a state of parallel polarization then it is absorbed. Otherwise, it is transmitted. Note that, in this example, the introduction of indeterminacy into the problem is clearly connected with the act of observation. In other words, the indeterminacy is related to the inevitable disturbance of the system associated with the act of observation.