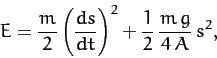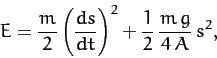Next: Planetary Motion
Up: Multi-Dimensional Motion
Previous: Charged Particle Motion in
- An electron of mass
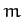 and charge
and charge 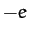 moves in a uniform
moves in a uniform  -directed electric field of magnitude
-directed electric field of magnitude 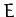 ,
and a uniform
,
and a uniform  -directed magnetic field of magnitude
-directed magnetic field of magnitude 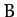 . The electron is situated at the
origin at
. The electron is situated at the
origin at  with an initial
with an initial  -directed velocity of magnitude
-directed velocity of magnitude  . Show that the
electron traces out a cycloid of the general form
. Show that the
electron traces out a cycloid of the general form
Find the values of 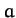 ,
, 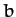 ,
, 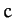 , and
, and 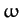 , and sketch the electron's trajectory
in the
, and sketch the electron's trajectory
in the  -
- plane when
plane when 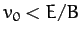 ,
,
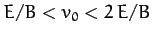 , and
, and
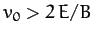 .
.
- A particle of mass
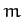 and charge
and charge 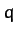 moves in the
moves in the  -
- plane
under the influence of a constant amplitude rotating electric field
which is such that
plane
under the influence of a constant amplitude rotating electric field
which is such that
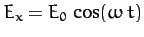 and
and
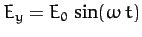 . The particle starts at rest from the origin. Determine its subsequent motion. What shape is the particle's trajectory?
. The particle starts at rest from the origin. Determine its subsequent motion. What shape is the particle's trajectory?
- A particle of mass
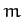 slides on a frictionless surface whose height is a
function of
slides on a frictionless surface whose height is a
function of  only: i.e.,
only: i.e., 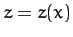 . The function
. The function 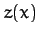 is specified by the parametric equations
is specified by the parametric equations
where 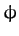 is the parameter. Show that the total energy of the
particle can be written
is the parameter. Show that the total energy of the
particle can be written
where
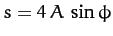 . Deduce that the particle undergoes periodic
motion whose frequency is amplitude independent (even when the amplitude
is large). Demonstrate that the frequency of the motion is given by
. Deduce that the particle undergoes periodic
motion whose frequency is amplitude independent (even when the amplitude
is large). Demonstrate that the frequency of the motion is given by
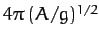 .
.



Next: Planetary Motion
Up: Multi-Dimensional Motion
Previous: Charged Particle Motion in
Richard Fitzpatrick
2011-03-31