


Next: Exercises
Up: Multi-Dimensional Motion
Previous: Projectile Motion with Air
Consider a particle of mass 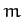 and electric charge
and electric charge 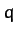 moving
in the uniform electric and magnetic fields,
moving
in the uniform electric and magnetic fields,  and
and 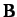 .
Suppose that the fields are ``crossed'' (i.e., perpendicular to
one another), so that
.
Suppose that the fields are ``crossed'' (i.e., perpendicular to
one another), so that
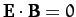 .
.
The force acting on the particle is given by the familiar Lorentz law:
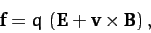 |
(194) |
where 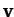 is the particle's instantaneous velocity. Hence, from
Newton's second law, the particle's equation of motion can be written
is the particle's instantaneous velocity. Hence, from
Newton's second law, the particle's equation of motion can be written
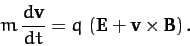 |
(195) |
It turns out that we can eliminate the electric field from the above equation by
transforming to a different inertial frame. Thus, writing
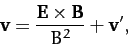 |
(196) |
Equation (195) reduces to
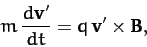 |
(197) |
where we have made use of a standard vector identity (see Section A.10), as well
as the fact that
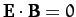 .
Hence, we conclude that the addition of an electric field perpendicular to a
given magnetic field simply causes the particle to drift perpendicular to both the electric and magnetic
field with the fixed velocity
.
Hence, we conclude that the addition of an electric field perpendicular to a
given magnetic field simply causes the particle to drift perpendicular to both the electric and magnetic
field with the fixed velocity
 |
(198) |
irrespective of its
charge or mass.
It follows that the electric field has no effect on the particle's
motion in a frame of reference which is co-moving with the so-called E-cross-B velocity given above.
Let us suppose that the magnetic field is directed along the  -axis.
As we have just seen, in the
-axis.
As we have just seen, in the
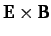 frame, the particle's equation of motion reduces to Equation (197), which can be written:
frame, the particle's equation of motion reduces to Equation (197), which can be written:
Here,
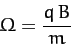 |
(202) |
is the so-called cyclotron frequency.
Equations (199)-(201) can be integrated to give
where we have judiciously chosen the origin of time so as to eliminate
any phase offset in the arguments of the above trigonometrical functions.
According to Equations (203)-(205), in the
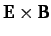 frame, our charged particle gyrates at the cyclotron frequency in the plane perpendicular to the
magnetic field with some fixed speed
frame, our charged particle gyrates at the cyclotron frequency in the plane perpendicular to the
magnetic field with some fixed speed 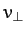 , and drifts parallel to the magnetic
field with some fixed speed
, and drifts parallel to the magnetic
field with some fixed speed 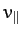 .
The fact that the cyclotron frequency is positive for positively charged
particles, and negative for negatively charged particles, just means that
oppositely charged particles gyrate in opposite directions in the
plane perpendicular to the magnetic field.
.
The fact that the cyclotron frequency is positive for positively charged
particles, and negative for negatively charged particles, just means that
oppositely charged particles gyrate in opposite directions in the
plane perpendicular to the magnetic field.
Equations (203)-(205) can be integrated to give
where we have judiciously chosen the origin of our coordinate system so
as to eliminate any constant offsets in the above equations.
Here,
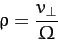 |
(209) |
is called the Larmor radius. Equations (206)-(208)
are the equations of a spiral of radius 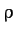 , aligned along the direction
of the magnetic field (i.e., the
, aligned along the direction
of the magnetic field (i.e., the  -direction).
-direction).
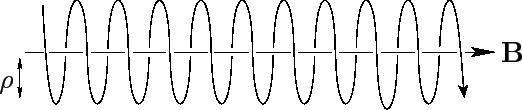
Figure 12:
The spiral trajectory of a negatively charged particle in a magnetic field.
 |
We conclude that the general motion of a charged particle in crossed
electric and magnetic field is a combination of
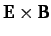 drift [see Equation (198)] and spiral motion aligned along the
direction of the magnetic field--see Figure 12. Particles drift parallel to the magnetic field
with constant speeds, and gyrate at the cyclotron frequency in the plane perpendicular to the magnetic field with constant speeds.
Oppositely charged particles gyrate in opposite directions.
drift [see Equation (198)] and spiral motion aligned along the
direction of the magnetic field--see Figure 12. Particles drift parallel to the magnetic field
with constant speeds, and gyrate at the cyclotron frequency in the plane perpendicular to the magnetic field with constant speeds.
Oppositely charged particles gyrate in opposite directions.



Next: Exercises
Up: Multi-Dimensional Motion
Previous: Projectile Motion with Air
Richard Fitzpatrick
2011-03-31
![]() -axis.
As we have just seen, in the
-axis.
As we have just seen, in the
![]() frame, the particle's equation of motion reduces to Equation (197), which can be written:
frame, the particle's equation of motion reduces to Equation (197), which can be written:
![]() drift [see Equation (198)] and spiral motion aligned along the
direction of the magnetic field--see Figure 12. Particles drift parallel to the magnetic field
with constant speeds, and gyrate at the cyclotron frequency in the plane perpendicular to the magnetic field with constant speeds.
Oppositely charged particles gyrate in opposite directions.
drift [see Equation (198)] and spiral motion aligned along the
direction of the magnetic field--see Figure 12. Particles drift parallel to the magnetic field
with constant speeds, and gyrate at the cyclotron frequency in the plane perpendicular to the magnetic field with constant speeds.
Oppositely charged particles gyrate in opposite directions.