


Next: Transients
Up: One-Dimensional Motion
Previous: Resonance
In the last section, we investigated the response of a one-dimensional dynamical system, close to a stable equilibrium point,
to an external force which varies as
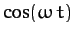 . Let us
now examine the response of the same system to a more complicated
external force.
. Let us
now examine the response of the same system to a more complicated
external force.
Consider a general external force which is periodic in time, with
period 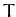 . By analogy with Equation (104), we can write such a
force as
. By analogy with Equation (104), we can write such a
force as
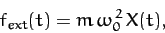 |
(115) |
where
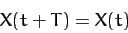 |
(116) |
for all 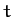 .
.
It is convenient to represent 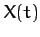 as a Fourier series in time, so that
as a Fourier series in time, so that
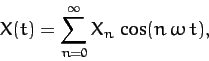 |
(117) |
where
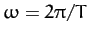 . By writing
. By writing 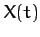 in this form, we automatically
satisfy the periodicity constraint (116). [Note that by choosing a cosine
Fourier series we are limited to even functions in
in this form, we automatically
satisfy the periodicity constraint (116). [Note that by choosing a cosine
Fourier series we are limited to even functions in 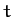 : i.e.,
: i.e., 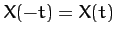 .
Odd functions in
.
Odd functions in 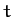 can be represented by sine Fourier series, and
mixed functions require a combination of cosine and sine Fourier series.]
The constant coefficients
can be represented by sine Fourier series, and
mixed functions require a combination of cosine and sine Fourier series.]
The constant coefficients
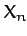 are known as Fourier coefficients. But,
how do we determine these coefficients for a given functional form,
are known as Fourier coefficients. But,
how do we determine these coefficients for a given functional form, 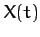 ?
?
Well, it follows from the periodicity of the cosine function that
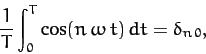 |
(118) |
where
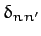 is unity if
is unity if 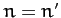 , and zero otherwise, and
is known as the Kronecker delta function.
Thus, integrating Equation (117)
in
, and zero otherwise, and
is known as the Kronecker delta function.
Thus, integrating Equation (117)
in 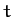 from
from  to
to 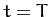 , and making use of Equation (118),
we obtain
, and making use of Equation (118),
we obtain
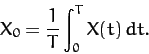 |
(119) |
It is also easily demonstrated that
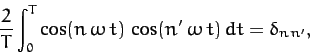 |
(120) |
provided 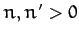 . Thus, multiplying Equation (117) by
. Thus, multiplying Equation (117) by
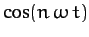 , integrating in
, integrating in 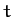 from
from  to
to 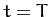 , and
making use of Equations (118) and (120), we obtain
, and
making use of Equations (118) and (120), we obtain
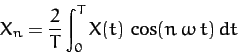 |
(121) |
for 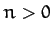 . Hence, we have now determined the Fourier coefficients of
the general periodic function
. Hence, we have now determined the Fourier coefficients of
the general periodic function 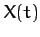 .
.
We can incorporate the periodic external force (115) into our
perturbed equation of motion by writing
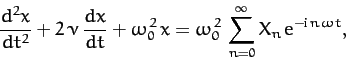 |
(122) |
where we are again using the convention that the physical solution
corresponds to the real part of the complex solution. Note that
the above differential equation is linear. This means that if 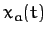 and
and 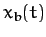 represent two independent solutions to this equation then
any linear combination of
represent two independent solutions to this equation then
any linear combination of 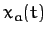 and
and 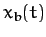 is also a solution. We can
exploit the linearity of the above equation to write the
solution in the form
is also a solution. We can
exploit the linearity of the above equation to write the
solution in the form
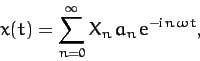 |
(123) |
where the 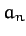 are the complex amplitudes of the solutions to
are the complex amplitudes of the solutions to
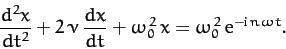 |
(124) |
In other words, 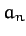 is obtained by substituting
is obtained by substituting
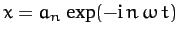 into the above equation.
Hence, it follows that
into the above equation.
Hence, it follows that
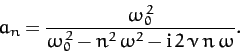 |
(125) |
Thus, the physical solution takes the form
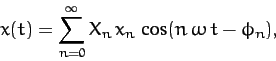 |
(126) |
where
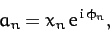 |
(127) |
and 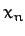 and
and 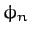 are real parameters. It follows from
Equation (125) that
are real parameters. It follows from
Equation (125) that
![\begin{displaymath}
x_n = \frac{\omega_0^{\,2}}{\left[(\omega_0^{\,2}-n^2\,\omega^2)^2
+ 4\,\nu^2\,n^2\,\omega^2\right]^{1/2}},
\end{displaymath}](img423.png) |
(128) |
and
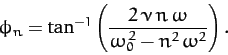 |
(129) |
We have now fully determined the response of our dynamical system to
a general periodic driving force.
As an example, suppose that the external force periodically delivers a brief kick to
the system. For instance, let
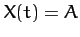 for
for
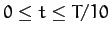 and
and 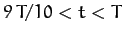 , and
, and 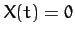 otherwise (in the period
otherwise (in the period 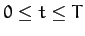 ).
It follows from Equation (119) and (121) that, in this case,
).
It follows from Equation (119) and (121) that, in this case,
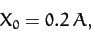 |
(130) |
and
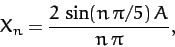 |
(131) |
for 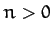 . Obviously, to obtain an exact solution, we would have to include
every Fourier harmonic in Equation (126), which would be impractical. However, we can obtain
a fairly accurate approximate solution by truncating the Fourier series (i.e.,
by neglecting all the terms with
. Obviously, to obtain an exact solution, we would have to include
every Fourier harmonic in Equation (126), which would be impractical. However, we can obtain
a fairly accurate approximate solution by truncating the Fourier series (i.e.,
by neglecting all the terms with 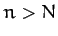 , where
, where 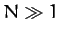 ).
).
Figure 7:
Periodic forcing.
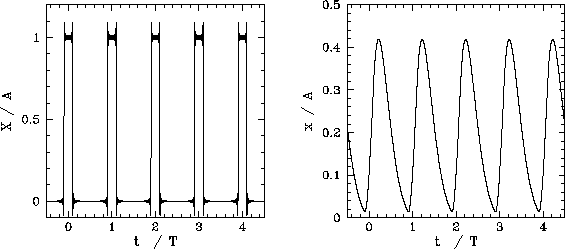 |
Figure 7 shows an example calculation in which the Fourier
series is truncated after 100 terms. The parameters used
in this calculation are
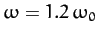 and
and
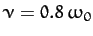 .
The left panel shows the Fourier reconstruction of the driving force,
.
The left panel shows the Fourier reconstruction of the driving force, 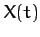 . The
glitches at the rising and falling edges of the pulses are called Gibbs
phenomena, and are an inevitable consequence of attempting to
represent a discontinuous periodic function as a Fourier series. The
right panel shows the Fourier reconstruction of the response,
. The
glitches at the rising and falling edges of the pulses are called Gibbs
phenomena, and are an inevitable consequence of attempting to
represent a discontinuous periodic function as a Fourier series. The
right panel shows the Fourier reconstruction of the response, 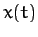 , of the dynamical
system to the applied force.
, of the dynamical
system to the applied force.



Next: Transients
Up: One-Dimensional Motion
Previous: Resonance
Richard Fitzpatrick
2011-03-31
![]() . By analogy with Equation (104), we can write such a
force as
. By analogy with Equation (104), we can write such a
force as
![]() as a Fourier series in time, so that
as a Fourier series in time, so that
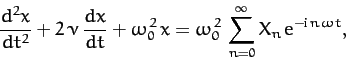
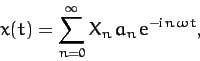
![\begin{displaymath}
x_n = \frac{\omega_0^{\,2}}{\left[(\omega_0^{\,2}-n^2\,\omega^2)^2
+ 4\,\nu^2\,n^2\,\omega^2\right]^{1/2}},
\end{displaymath}](img423.png)
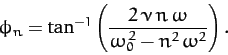
![]() for
for
![]() and
and ![]() , and
, and ![]() otherwise (in the period
otherwise (in the period ![]() ).
It follows from Equation (119) and (121) that, in this case,
).
It follows from Equation (119) and (121) that, in this case,
![]() and
and
![]() .
The left panel shows the Fourier reconstruction of the driving force,
.
The left panel shows the Fourier reconstruction of the driving force, ![]() . The
glitches at the rising and falling edges of the pulses are called Gibbs
phenomena, and are an inevitable consequence of attempting to
represent a discontinuous periodic function as a Fourier series. The
right panel shows the Fourier reconstruction of the response,
. The
glitches at the rising and falling edges of the pulses are called Gibbs
phenomena, and are an inevitable consequence of attempting to
represent a discontinuous periodic function as a Fourier series. The
right panel shows the Fourier reconstruction of the response, ![]() , of the dynamical
system to the applied force.
, of the dynamical
system to the applied force.