


Next: Coupled Oscillations
Up: Hamiltonian Dynamics
Previous: Hamilton's Equations
- A particle of mass
 is placed at the top of
a smooth vertical hoop of radius
is placed at the top of
a smooth vertical hoop of radius 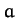 . Calculate the reaction of the hoop on the
particle as it slides down the hoop by means of the method of Lagrange multipliers. Find the height at which the particle falls off the hoop.
. Calculate the reaction of the hoop on the
particle as it slides down the hoop by means of the method of Lagrange multipliers. Find the height at which the particle falls off the hoop.
- A uniform disk of mass
 and radius
and radius 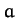 has a light string wrapped
around its circumference with one end of the string attached to a fixed
support. The disk is allowed to fall under gravity, unwinding the string
as it falls. Solve the problem using the method of Lagrange multipliers.
What is the tension in the string?
has a light string wrapped
around its circumference with one end of the string attached to a fixed
support. The disk is allowed to fall under gravity, unwinding the string
as it falls. Solve the problem using the method of Lagrange multipliers.
What is the tension in the string?
- Consider two particles of masses
 and
and 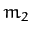 . Let
. Let  be constrained to move on a circle of radius
be constrained to move on a circle of radius 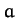 in the
in the 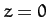 plane,
centered at
plane,
centered at 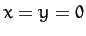 . (Here,
. (Here, 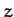 measures vertical height). Let
measures vertical height). Let 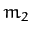 be constrained to move on a circle of radius
be constrained to move on a circle of radius 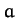 in the
in the 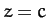 plane,
centered on
plane,
centered on 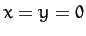 . A light spring of spring constant
. A light spring of spring constant 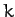 and unstretched
length
and unstretched
length 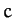 is attached between the particles. Find the Lagrangian of the system. Solve the
problem using Lagrange multipliers and give a physical interpretation
for each multiplier.
is attached between the particles. Find the Lagrangian of the system. Solve the
problem using Lagrange multipliers and give a physical interpretation
for each multiplier.
- Find the Hamiltonian of a particle of mass
 constrained to
move under gravity on the inside of a sphere of radius
constrained to
move under gravity on the inside of a sphere of radius 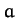 .
Use the standard spherical polar coordinates
.
Use the standard spherical polar coordinates  and
and 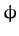 as
your generalized coordinates, where the axis of the coordinates points
vertically downward. Find Hamilton's equations of motion for the system.
as
your generalized coordinates, where the axis of the coordinates points
vertically downward. Find Hamilton's equations of motion for the system.
- A particle of mass
 is subject to a central attractive force
given by
is subject to a central attractive force
given by
where 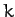 and
and 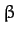 are positive constants. Find the Hamiltonian of
the particle. Compare the Hamiltonian to the total energy of the particle.
Is the energy of the particle conserved?
are positive constants. Find the Hamiltonian of
the particle. Compare the Hamiltonian to the total energy of the particle.
Is the energy of the particle conserved?



Next: Coupled Oscillations
Up: Hamiltonian Dynamics
Previous: Hamilton's Equations
Richard Fitzpatrick
2011-03-31