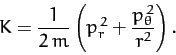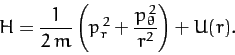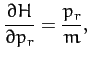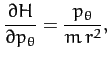Next: Exercises
Up: Hamiltonian Dynamics
Previous: Constrained Lagrangian Dynamics
Consider a dynamical system with 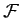 degrees of freedom which is described
by the generalized coordinates
degrees of freedom which is described
by the generalized coordinates 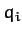 , for
, for 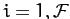 . Suppose that
neither the kinetic energy,
. Suppose that
neither the kinetic energy, 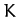 , nor the potential energy,
, nor the potential energy, 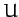 , depend
explicitly on the time,
, depend
explicitly on the time, 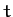 . Now, in conventional dynamical systems, the potential energy is generally independent of the
. Now, in conventional dynamical systems, the potential energy is generally independent of the 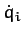 , whereas the kinetic
energy takes the form of a homogeneous quadratic function of
the
, whereas the kinetic
energy takes the form of a homogeneous quadratic function of
the 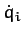 . In other words,
. In other words,
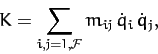 |
(744) |
where the 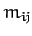 depend on the
depend on the 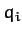 , but not on the
, but not on the 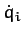 .
It is easily demonstrated from the above equation that
.
It is easily demonstrated from the above equation that
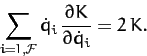 |
(745) |
Recall, from Section 9.8, that generalized momentum conjugate to the 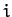 th
generalized coordinate is defined
th
generalized coordinate is defined
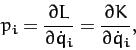 |
(746) |
where 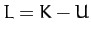 is the Lagrangian of the system, and we have made use of the fact that
is the Lagrangian of the system, and we have made use of the fact that 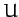 is independent of the
is independent of the 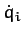 . Consider the
function
. Consider the
function
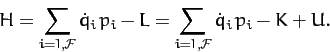 |
(747) |
If all of the conditions discussed above are satisfied then Equations (745)
and (746)
yield
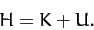 |
(748) |
In other words, the function 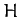 is equal to the total energy of the system.
is equal to the total energy of the system.
Consider the variation of the function 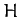 . We have
. We have
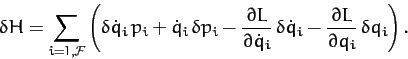 |
(749) |
The first and third terms in the bracket cancel, because
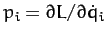 . Furthermore, since Lagrange's equation
can be written
. Furthermore, since Lagrange's equation
can be written
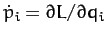 (see Section 9.8), we obtain
(see Section 9.8), we obtain
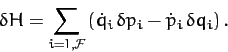 |
(750) |
Suppose, now, that we can express the total energy of the system,  , solely
as a function of the
, solely
as a function of the  and the
and the 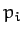 , with no explicit
dependence on the
, with no explicit
dependence on the 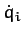 . In other words, suppose that we
can write
. In other words, suppose that we
can write 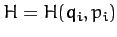 . When the energy is written
in this fashion it is generally termed the Hamiltonian of the system. The variation of the Hamiltonian function takes the form
. When the energy is written
in this fashion it is generally termed the Hamiltonian of the system. The variation of the Hamiltonian function takes the form
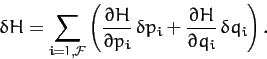 |
(751) |
A comparison of the previous two equations yields
for 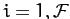 . These
. These 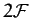 first-order differential equations are known
as Hamilton's equations. Hamilton's equations are often a
useful alternative to Lagrange's equations, which take the
form of
first-order differential equations are known
as Hamilton's equations. Hamilton's equations are often a
useful alternative to Lagrange's equations, which take the
form of 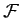 second-order differential equations.
second-order differential equations.
Consider a one-dimensional harmonic oscillator. The kinetic and potential
energies of the system are written
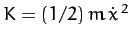 and
and
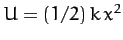 , where
, where  is the displacement,
is the displacement, 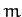 the mass, and
the mass, and 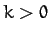 .
The generalized momentum conjugate to
.
The generalized momentum conjugate to  is
is
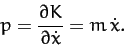 |
(754) |
Hence, we can write
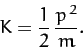 |
(755) |
So, the Hamiltonian of the system takes the form
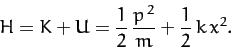 |
(756) |
Thus, Hamilton's equations, (752) and (753), yield
Of course, the first equation is just a restatement of Equation (754), whereas the second is Newton's second law of motion for the
system.
Consider a particle of mass 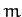 moving in the central potential
moving in the central potential 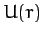 .
In this case,
.
In this case,
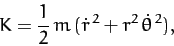 |
(759) |
where 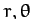 are polar coordinates. The generalized momenta conjugate to
are polar coordinates. The generalized momenta conjugate to 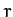 and
and 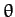 are
are
respectively.
Hence, we can write
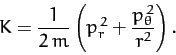 |
(762) |
Thus, the Hamiltonian of the system takes the form
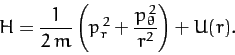 |
(763) |
In this case, Hamilton's equations yield
which are just restatements of Equations (760) and (761), respectively,
as well as
The last equation implies that
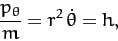 |
(768) |
where 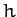 is a constant. This can be combined with Equation (766)
to give
is a constant. This can be combined with Equation (766)
to give
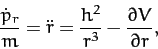 |
(769) |
where 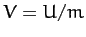 . Of course, Equations (768) and (769) are the
conventional equations of motion for a particle moving in a central potential--see Chapter 5.
. Of course, Equations (768) and (769) are the
conventional equations of motion for a particle moving in a central potential--see Chapter 5.



Next: Exercises
Up: Hamiltonian Dynamics
Previous: Constrained Lagrangian Dynamics
Richard Fitzpatrick
2011-03-31
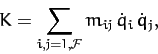
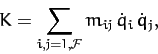
![]() th
generalized coordinate is defined
th
generalized coordinate is defined
![]() . We have
. We have
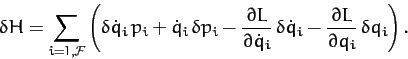
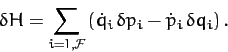
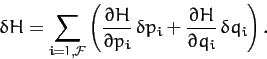
![]() and
and
![]() , where
, where ![]() is the displacement,
is the displacement, ![]() the mass, and
the mass, and ![]() .
The generalized momentum conjugate to
.
The generalized momentum conjugate to ![]() is
is
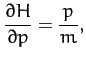
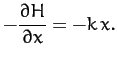
![]() moving in the central potential
moving in the central potential ![]() .
In this case,
.
In this case,