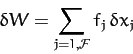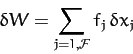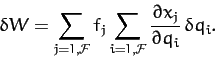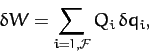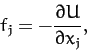Next: Lagrange's Equation
Up: Lagrangian Dynamics
Previous: Generalized Coordinates
The work done on the dynamical system when its Cartesian coordinates
change by 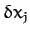 is simply
is simply
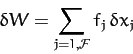 |
(594) |
Here, the 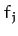 are the Cartesian components of the forces acting on the
various particles making up the system. Thus,
are the Cartesian components of the forces acting on the
various particles making up the system. Thus, 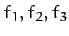 are the
components of the force acting on the first particle,
are the
components of the force acting on the first particle, 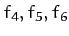 the components of the force acting on the second particle, etc.
Using Equation (593), we can also write
the components of the force acting on the second particle, etc.
Using Equation (593), we can also write
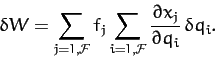 |
(595) |
The above expression can be rearranged to give
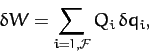 |
(596) |
where
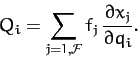 |
(597) |
Here, the 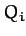 are termed generalized forces. Note that a generalized
force does not necessarily have the dimensions of force. However, the
product
are termed generalized forces. Note that a generalized
force does not necessarily have the dimensions of force. However, the
product 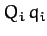 must have the dimensions of work. Thus, if
a particular
must have the dimensions of work. Thus, if
a particular 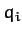 is a Cartesian coordinate then the associated
is a Cartesian coordinate then the associated 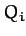 is a force.
Conversely, if a particular
is a force.
Conversely, if a particular 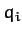 is an angle then the associated
is an angle then the associated 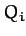 is a torque.
is a torque.
Suppose that the dynamical system in question is conservative. It follows that
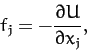 |
(598) |
for 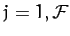 , where
, where
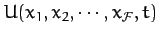 is the system's potential energy. Hence, according to Equation (597),
is the system's potential energy. Hence, according to Equation (597),
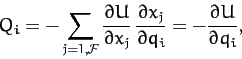 |
(599) |
for 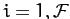 .
.



Next: Lagrange's Equation
Up: Lagrangian Dynamics
Previous: Generalized Coordinates
Richard Fitzpatrick
2011-03-31