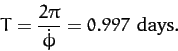Next: Gyroscopic Precession
Up: Rigid Body Rotation
Previous: Euler's Equations
Eulerian Angles
We have seen how we can solve Euler's equations to determine the properties
of a rotating body in the co-rotating body frame. Let us now investigate how we can determine the same properties in the inertial
fixed frame.
The fixed frame and the body frame share the
same origin. Hence, we can transform from one to the other by
means of an appropriate rotation of our coordinate axes.
In general, if we restrict ourselves to rotations about one of the Cartesian
axes, three successive rotations are required to
transform the fixed frame into the body frame. There are, in fact, many different
ways to combined three successive rotations in order to achieve this. In the following, we shall describe the
most widely used method, which is due to Euler.
We start in the fixed frame, which has coordinates 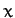 ,
, 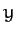 ,
, 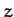 , and
unit vectors
, and
unit vectors 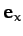 ,
, 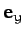 ,
,  . Our first rotation
is counterclockwise (looking down the axis) through an angle
. Our first rotation
is counterclockwise (looking down the axis) through an angle 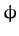 about the
about the 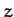 -axis. The new frame has coordinates
-axis. The new frame has coordinates 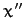 ,
, 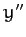 ,
, 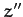 , and
unit vectors
, and
unit vectors 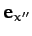 ,
, 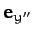 ,
,  . According
to Equations (A.1277)-(A.1279), the transformation of coordinates can be represented as
follows:
. According
to Equations (A.1277)-(A.1279), the transformation of coordinates can be represented as
follows:
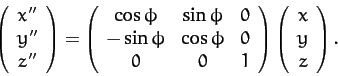 |
(528) |
The angular velocity vector associated with 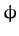 has the magnitude
has the magnitude 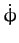 ,
and is directed along
,
and is directed along  (i.e., along the axis of rotation).
Hence, we can write
(i.e., along the axis of rotation).
Hence, we can write
 |
(529) |
Clearly, 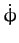 is the precession rate about the
is the precession rate about the  axis,
as seen in the fixed frame.
axis,
as seen in the fixed frame.
The second rotation is counterclockwise (looking down the axis) through
an angle  about the
about the 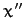 -axis. The new frame has coordinates
-axis. The new frame has coordinates
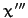 ,
, 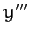 ,
, 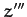 , and unit vectors
, and unit vectors
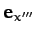 ,
,
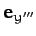 ,
,
 . By analogy with Equation (528), the transformation
of coordinates can be represented as follows:
. By analogy with Equation (528), the transformation
of coordinates can be represented as follows:
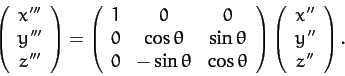 |
(530) |
The angular velocity vector associated with  has the magnitude
has the magnitude  ,
and is directed along
,
and is directed along 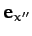 (i.e., along the axis of rotation).
Hence, we can write
(i.e., along the axis of rotation).
Hence, we can write
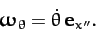 |
(531) |
The third rotation is counterclockwise (looking down the axis) through
an angle 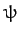 about the
about the 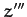 -axis. The new frame is the body frame, which has coordinates
-axis. The new frame is the body frame, which has coordinates
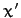 ,
,  ,
, 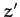 , and unit vectors
, and unit vectors 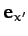 ,
, 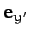 ,
, 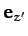 . The transformation of coordinates can be represented as
follows:
. The transformation of coordinates can be represented as
follows:
 |
(532) |
The angular velocity vector associated with 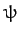 has the magnitude
has the magnitude  ,
and is directed along
,
and is directed along  (i.e., along the axis of rotation).
Note that
(i.e., along the axis of rotation).
Note that
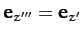 , since the third rotation is about
, since the third rotation is about
 .
Hence, we can write
.
Hence, we can write
 |
(533) |
Clearly,  is minus the precession rate about the
is minus the precession rate about the 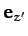 axis, as seen in the body frame.
axis, as seen in the body frame.
The full transformation between the fixed frame and the body frame
is rather complicated. However, the following results can easily be
verified:
It follows from Equation (534) that
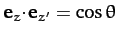 . In other words,
. In other words,  is the angle of inclination between the
is the angle of inclination between the
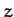 - and
- and 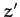 -axes.
Finally, since the total angular velocity can be written
-axes.
Finally, since the total angular velocity can be written
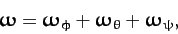 |
(536) |
Equations (529), (531), and (533)-(535)
yield
The angles 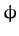 ,
,  , and
, and 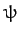 are termed Eulerian angles. Each has a clear physical interpretation:
are termed Eulerian angles. Each has a clear physical interpretation: 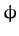 is the angle of precession
about the
is the angle of precession
about the  axis in the fixed frame,
axis in the fixed frame, 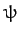 is minus the angle of precession about the
is minus the angle of precession about the
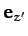 axis in the body frame, and
axis in the body frame, and  is the angle of inclination
between the
is the angle of inclination
between the  and
and 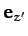 axes. Moreover, we can
express the components of the angular velocity vector
axes. Moreover, we can
express the components of the angular velocity vector 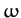 in the body frame entirely in terms of the Eulerian angles, and their time derivatives [see Equations (537)-(539)].
in the body frame entirely in terms of the Eulerian angles, and their time derivatives [see Equations (537)-(539)].
Consider a rigid body which is constrained to rotate about a fixed axis with
the constant angular velocity 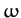 . Let the fixed angular velocity
vector point along the
. Let the fixed angular velocity
vector point along the 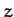 -axis. In the previous section, we saw that
the angular momentum and the torque were both steady in the body frame.
Since there is no precession of quantities in the body frame, it follows that
the Eulerian angle
-axis. In the previous section, we saw that
the angular momentum and the torque were both steady in the body frame.
Since there is no precession of quantities in the body frame, it follows that
the Eulerian angle 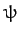 is constant. Furthermore, since the angular velocity vector is
fixed in the body frame, as well as the fixed frame [as can be seen by applying Equation (502)
to
is constant. Furthermore, since the angular velocity vector is
fixed in the body frame, as well as the fixed frame [as can be seen by applying Equation (502)
to 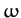 instead of
instead of 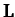 ], it must subtend a constant angle with the
], it must subtend a constant angle with the
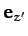 axis. Hence, the Eulerian angle
axis. Hence, the Eulerian angle  is also constant.
It follows from Equations (537)-(539) that
is also constant.
It follows from Equations (537)-(539) that
which implies that
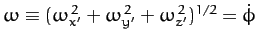 . In other words, the precession
rate,
. In other words, the precession
rate, 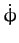 , in the fixed frame is equal to
, in the fixed frame is equal to 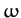 . Hence, in the fixed frame,
the constant torque and angular momentum vectors found in the body
frame precess about the angular velocity vector (i.e., about the
. Hence, in the fixed frame,
the constant torque and angular momentum vectors found in the body
frame precess about the angular velocity vector (i.e., about the
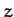 -axis) at the rate
-axis) at the rate 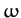 . As discussed in the previous section, for the special case where the angular
velocity vector is parallel to one of the principal axes of the body, the angular
momentum vector is parallel to the angular velocity vector, and the torque is zero. Thus,
in this case, there is no precession in the fixed frame.
. As discussed in the previous section, for the special case where the angular
velocity vector is parallel to one of the principal axes of the body, the angular
momentum vector is parallel to the angular velocity vector, and the torque is zero. Thus,
in this case, there is no precession in the fixed frame.
Consider a rotating device such as a flywheel or a propeller. If the device
is statically balanced then its center of mass lies on the axis
of rotation. This is desirable since, otherwise, gravity, which effectively
acts at the center of mass, exerts a varying torque about the
axis of rotation as the device rotates, giving rise to unsteady rotation. If the device is
dynamically balanced then the axis of rotation is also
a principal axis, so that, as the device rotates its angular momentum vector,
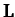 ,
remains parallel to the axis of rotation. This is desirable since, otherwise,
the angular momentum vector is not parallel to the axis of rotation, and, therefore, precesses around it. Since
,
remains parallel to the axis of rotation. This is desirable since, otherwise,
the angular momentum vector is not parallel to the axis of rotation, and, therefore, precesses around it. Since 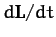 is equal to the
torque, a precessing torque must also be applied to the device (at right-angles
to both the axis and
is equal to the
torque, a precessing torque must also be applied to the device (at right-angles
to both the axis and 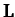 ). The result is a reaction
on the bearings which can give rise to violent vibration and
wobbling, even when the device is statically balanced.
). The result is a reaction
on the bearings which can give rise to violent vibration and
wobbling, even when the device is statically balanced.
Consider a freely rotating body which is rotationally symmetric about one axis (the 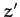 -axis). In the absence of an external torque, the
angular momentum vector
-axis). In the absence of an external torque, the
angular momentum vector 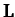 is a constant of the motion [see Equation (456)]. Let
is a constant of the motion [see Equation (456)]. Let 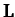 point along the
point along the 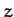 -axis. In the
previous section, we saw that the angular momentum vector subtends a
constant angle
-axis. In the
previous section, we saw that the angular momentum vector subtends a
constant angle  with the axis of symmetry: i.e., with the
with the axis of symmetry: i.e., with the 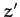 -axis. Hence, the time derivative
of the Eulerian angle
-axis. Hence, the time derivative
of the Eulerian angle  is zero. We also saw that the angular momentum
vector, the axis of symmetry, and the angular velocity vector are coplanar.
Consider an instant in time at which all of these vectors lie in the
is zero. We also saw that the angular momentum
vector, the axis of symmetry, and the angular velocity vector are coplanar.
Consider an instant in time at which all of these vectors lie in the  -
-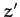 plane. This implies that
plane. This implies that 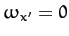 . According to the
previous section, the angular velocity vector subtends a constant
angle
. According to the
previous section, the angular velocity vector subtends a constant
angle 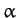 with the symmetry axis. It follows that
with the symmetry axis. It follows that
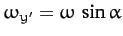 and
and
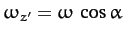 . Equation (537) yields
. Equation (537) yields
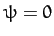 . Hence, Equation (538) yields
. Hence, Equation (538) yields
 |
(543) |
This can be combined with Equation (525) to give
![\begin{displaymath}
\dot{\phi} = \omega\left[1 + \left(\frac{I_\parallel^{\,2}}{I_\perp^{\,2}}-1\right)\cos^2\alpha\right]^{1/2}.
\end{displaymath}](img1459.png) |
(544) |
Finally, Equations (539), together with (525) and (543),
yields
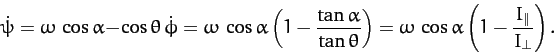 |
(545) |
A comparison of the above equation with Equation (521) gives
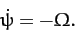 |
(546) |
Thus, as expected,  is minus the precession rate (of the angular
momentum and angular velocity vectors) in the body frame. On the other hand,
is minus the precession rate (of the angular
momentum and angular velocity vectors) in the body frame. On the other hand, 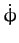 is the precession rate (of the angular velocity vector
and the symmetry axis) in the
fixed frame. Note that
is the precession rate (of the angular velocity vector
and the symmetry axis) in the
fixed frame. Note that 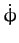 and
and  are
quite dissimilar. For instance,
are
quite dissimilar. For instance,  is negative for elongated
bodies (
is negative for elongated
bodies (
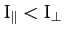 ) whereas
) whereas 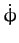 is positive definite. It follows that the precession is always in the
same sense as
is positive definite. It follows that the precession is always in the
same sense as 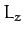 in the fixed frame, whereas the
precession in the body frame is in the opposite sense to
in the fixed frame, whereas the
precession in the body frame is in the opposite sense to 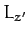 for elongated bodies. We
found, in the previous section, that for a flattened body the angular
momentum vector lies between the angular velocity vector and the symmetry
axis. This means that, in the fixed frame, the angular velocity vector
and the symmetry axis lie on opposite sides of the fixed angular
momentum vector. On the other hand, for an elongated body
we found that the angular velocity vector lies between the angular momentum
vector and the symmetry axis. This means that, in the fixed frame, the
angular velocity vector and the symmetry axis lie on the same side of
the fixed angular momentum vector. (Recall that the angular
momentum vector, the angular velocity vector, and the symmetry
axis, are coplanar.)
for elongated bodies. We
found, in the previous section, that for a flattened body the angular
momentum vector lies between the angular velocity vector and the symmetry
axis. This means that, in the fixed frame, the angular velocity vector
and the symmetry axis lie on opposite sides of the fixed angular
momentum vector. On the other hand, for an elongated body
we found that the angular velocity vector lies between the angular momentum
vector and the symmetry axis. This means that, in the fixed frame, the
angular velocity vector and the symmetry axis lie on the same side of
the fixed angular momentum vector. (Recall that the angular
momentum vector, the angular velocity vector, and the symmetry
axis, are coplanar.)
As an example, consider the free rotation of a thin disk. It is easily
demonstrated (from the perpendicular axis theorem)
that
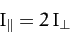 |
(547) |
for such a disk. Hence, from Equation (521), the precession rate in the
body frame is
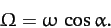 |
(548) |
According to Equation (544), the precession rate in the fixed frame is
![\begin{displaymath}
\dot{\phi} = \omega\left[1+ 3\,\cos^2\alpha\right]^{1/2}.
\end{displaymath}](img1467.png) |
(549) |
In the limit in which 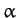 is small (i.e., in which the
angular velocity vector is almost parallel to the symmetry axis),
we obtain
is small (i.e., in which the
angular velocity vector is almost parallel to the symmetry axis),
we obtain
Thus, the symmetry axis precesses in the fixed frame at approximately
twice the angular speed of rotation. This precession is manifest as
a wobbling motion.
It is known that the axis of rotation of the Earth is very slightly inclined to
its symmetry axis (which passes through the two geographic poles). The angle 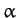 is approximately
is approximately 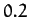 seconds of an arc
(which corresponds to a distance of about
seconds of an arc
(which corresponds to a distance of about 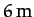 on the Earth's surface).
It is also known that the ratio of the terrestrial moments of inertia
is about
on the Earth's surface).
It is also known that the ratio of the terrestrial moments of inertia
is about
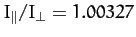 , as determined from the
Earth's oblateness--see Section 12.7. Hence, from (521), the precession rate of the
angular velocity vector about the symmetry axis, as viewed in a geostationary reference frame, is
, as determined from the
Earth's oblateness--see Section 12.7. Hence, from (521), the precession rate of the
angular velocity vector about the symmetry axis, as viewed in a geostationary reference frame, is
 |
(552) |
giving a precession period of
 |
(553) |
(Of course,
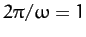 day.)
The observed period of precession is about 440 days. The disagreement
between theory and observation is attributed to the fact that the Earth
is not perfectly rigid.
The Earth's symmetry axis subtends an angle
day.)
The observed period of precession is about 440 days. The disagreement
between theory and observation is attributed to the fact that the Earth
is not perfectly rigid.
The Earth's symmetry axis subtends an angle
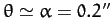 [see (525)] with
its angular momentum vector, but lies on the opposite side of this vector to the angular velocity vector.
This implies that, as viewed from space, the Earth's angular velocity vector is almost parallel to its
fixed angular momentum vector, whereas its symmetry axis subtends an angle of
[see (525)] with
its angular momentum vector, but lies on the opposite side of this vector to the angular velocity vector.
This implies that, as viewed from space, the Earth's angular velocity vector is almost parallel to its
fixed angular momentum vector, whereas its symmetry axis subtends an angle of 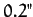 with both vectors, and
precesses about them.
The (theoretical) precession rate of the Earth's symmetry
axis, as seen from space, is given by Equation (544):
with both vectors, and
precesses about them.
The (theoretical) precession rate of the Earth's symmetry
axis, as seen from space, is given by Equation (544):
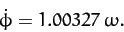 |
(554) |
The associated precession period is
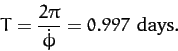 |
(555) |
The free precession of the Earth's symmetry axis in space, which is known as the Chandler wobble, since it
was discovered by the American astronomer Seth Chandler in 1891,
is superimposed on
a much slower forced precession, with a period of about 26,000 years, caused by
the small gravitational torque exerted on the Earth by the Sun and the
Moon, as a consequence of the Earth's slight oblateness--see Section 12.10.



Next: Gyroscopic Precession
Up: Rigid Body Rotation
Previous: Euler's Equations
Richard Fitzpatrick
2011-03-31
![]() ,
, ![]() ,
, ![]() , and
unit vectors
, and
unit vectors ![]() ,
, ![]() ,
, ![]() . Our first rotation
is counterclockwise (looking down the axis) through an angle
. Our first rotation
is counterclockwise (looking down the axis) through an angle ![]() about the
about the ![]() -axis. The new frame has coordinates
-axis. The new frame has coordinates ![]() ,
, ![]() ,
, ![]() , and
unit vectors
, and
unit vectors ![]() ,
, ![]() ,
, ![]() . According
to Equations (A.1277)-(A.1279), the transformation of coordinates can be represented as
follows:
. According
to Equations (A.1277)-(A.1279), the transformation of coordinates can be represented as
follows:
![]() about the
about the ![]() -axis. The new frame has coordinates
-axis. The new frame has coordinates
![]() ,
, ![]() ,
, ![]() , and unit vectors
, and unit vectors
![]() ,
,
![]() ,
,
![]() . By analogy with Equation (528), the transformation
of coordinates can be represented as follows:
. By analogy with Equation (528), the transformation
of coordinates can be represented as follows:
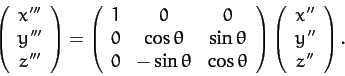
![]() about the
about the ![]() -axis. The new frame is the body frame, which has coordinates
-axis. The new frame is the body frame, which has coordinates
![]() ,
, ![]() ,
, ![]() , and unit vectors
, and unit vectors ![]() ,
, ![]() ,
, ![]() . The transformation of coordinates can be represented as
follows:
. The transformation of coordinates can be represented as
follows:

![]() ,
, ![]() , and
, and ![]() are termed Eulerian angles. Each has a clear physical interpretation:
are termed Eulerian angles. Each has a clear physical interpretation: ![]() is the angle of precession
about the
is the angle of precession
about the ![]() axis in the fixed frame,
axis in the fixed frame, ![]() is minus the angle of precession about the
is minus the angle of precession about the
![]() axis in the body frame, and
axis in the body frame, and ![]() is the angle of inclination
between the
is the angle of inclination
between the ![]() and
and ![]() axes. Moreover, we can
express the components of the angular velocity vector
axes. Moreover, we can
express the components of the angular velocity vector ![]() in the body frame entirely in terms of the Eulerian angles, and their time derivatives [see Equations (537)-(539)].
in the body frame entirely in terms of the Eulerian angles, and their time derivatives [see Equations (537)-(539)].
![]() . Let the fixed angular velocity
vector point along the
. Let the fixed angular velocity
vector point along the ![]() -axis. In the previous section, we saw that
the angular momentum and the torque were both steady in the body frame.
Since there is no precession of quantities in the body frame, it follows that
the Eulerian angle
-axis. In the previous section, we saw that
the angular momentum and the torque were both steady in the body frame.
Since there is no precession of quantities in the body frame, it follows that
the Eulerian angle ![]() is constant. Furthermore, since the angular velocity vector is
fixed in the body frame, as well as the fixed frame [as can be seen by applying Equation (502)
to
is constant. Furthermore, since the angular velocity vector is
fixed in the body frame, as well as the fixed frame [as can be seen by applying Equation (502)
to ![]() instead of
instead of ![]() ], it must subtend a constant angle with the
], it must subtend a constant angle with the
![]() axis. Hence, the Eulerian angle
axis. Hence, the Eulerian angle ![]() is also constant.
It follows from Equations (537)-(539) that
is also constant.
It follows from Equations (537)-(539) that
![]() ,
remains parallel to the axis of rotation. This is desirable since, otherwise,
the angular momentum vector is not parallel to the axis of rotation, and, therefore, precesses around it. Since
,
remains parallel to the axis of rotation. This is desirable since, otherwise,
the angular momentum vector is not parallel to the axis of rotation, and, therefore, precesses around it. Since ![]() is equal to the
torque, a precessing torque must also be applied to the device (at right-angles
to both the axis and
is equal to the
torque, a precessing torque must also be applied to the device (at right-angles
to both the axis and ![]() ). The result is a reaction
on the bearings which can give rise to violent vibration and
wobbling, even when the device is statically balanced.
). The result is a reaction
on the bearings which can give rise to violent vibration and
wobbling, even when the device is statically balanced.
![]() -axis). In the absence of an external torque, the
angular momentum vector
-axis). In the absence of an external torque, the
angular momentum vector ![]() is a constant of the motion [see Equation (456)]. Let
is a constant of the motion [see Equation (456)]. Let ![]() point along the
point along the ![]() -axis. In the
previous section, we saw that the angular momentum vector subtends a
constant angle
-axis. In the
previous section, we saw that the angular momentum vector subtends a
constant angle ![]() with the axis of symmetry: i.e., with the
with the axis of symmetry: i.e., with the ![]() -axis. Hence, the time derivative
of the Eulerian angle
-axis. Hence, the time derivative
of the Eulerian angle ![]() is zero. We also saw that the angular momentum
vector, the axis of symmetry, and the angular velocity vector are coplanar.
Consider an instant in time at which all of these vectors lie in the
is zero. We also saw that the angular momentum
vector, the axis of symmetry, and the angular velocity vector are coplanar.
Consider an instant in time at which all of these vectors lie in the ![]() -
-![]() plane. This implies that
plane. This implies that ![]() . According to the
previous section, the angular velocity vector subtends a constant
angle
. According to the
previous section, the angular velocity vector subtends a constant
angle ![]() with the symmetry axis. It follows that
with the symmetry axis. It follows that
![]() and
and
![]() . Equation (537) yields
. Equation (537) yields
![]() . Hence, Equation (538) yields
. Hence, Equation (538) yields
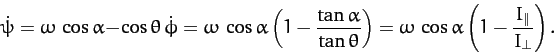
![]() is approximately
is approximately ![]() seconds of an arc
(which corresponds to a distance of about
seconds of an arc
(which corresponds to a distance of about ![]() on the Earth's surface).
It is also known that the ratio of the terrestrial moments of inertia
is about
on the Earth's surface).
It is also known that the ratio of the terrestrial moments of inertia
is about
![]() , as determined from the
Earth's oblateness--see Section 12.7. Hence, from (521), the precession rate of the
angular velocity vector about the symmetry axis, as viewed in a geostationary reference frame, is
, as determined from the
Earth's oblateness--see Section 12.7. Hence, from (521), the precession rate of the
angular velocity vector about the symmetry axis, as viewed in a geostationary reference frame, is